Geração de números não uniformes
Método de aceitação e rejeição
Walmes M. Zeviani e Fernando P. Mayer
1 Introdução
Quando se deseja gerar números aleatórios de distribuições de probabilidade, nem sempre é possível aplicar o método da transformação integral da probabilidade. Alguns situação são:
- Casos em que não se tem expressão para a função de densidade acumulada \(F(x)\)
- Casos em que mesmo que se conheça \(F(x)\) não possível chegar à uma expressão para a função \(F^{-1}(x)\).
2 Método de aceitação e rejeição
Se a função densidade de probabilidade for conhecida, \(f\), então é possível gerar números aleatórios dessa variável aleatória caracterizada por \(f\) pelo método da aceitação e rejeição. É necessário satisfazer dois requisitos:
- Ter um bom gerador de números uniformes.
- Ter um bom gerador de números de uma variável aleatória representada por uma distribuição \(D\), escolhida de tal maneira que existe uma constante \(M\) tal que a densidade de \(g\) que caracteriza a distribuição \(D\) satisfaz \[ f(x) \leq M g(x) \] para todo \(x\) do domínio de \(f\). A função \(g\) que “encapsula” a função \(f\) é chamada de distribuição proposta (proposal).
O seguinte algoritmo permite gerar números aleatórios de uma distribuição de probabilidade caracterizada pela função densidade \(f\):
- Gerar \(y\) como sendo uma ocorrência da variável aleatória representada por \(D\).
- Gerar \(u\) como sendo uma ocorrência de uma uniforme padrão.
- Se \[ u \leq \frac{f(y)}{M g(y)} \] considerar que \(x = y\) é um valor da distribuição de probabilidade alvo cuja densidade é \(f\), caso contrário, descartar \(y\).
- Repetir até atingir o número de valores desejado \(n\).
Para determinar o valor de \(M\), basta seguir a seguinte relação
\[ M \geq \max_x \frac{f(x)}{g(x)} \]
Alguns pontos que devem ser levados em consideração:
- O limite \(f(x) \leq M g(x)\) não precisa ser tão pequeno. O algoritmo permanece válido (mas possivelmente menos eficiente) quando \(M\) for um valor maior
- A probabilidade de aceitação é \(1/M\). Portanto \(M\) deve ser o menor possível para maior eficiência computacional.
2.1 Exemplo 1
Seja \(X\) uma VA com \(f(x) = 1.5 x^2, -1 < x < 1\). Simular valores desta distribuição.
## Gráfico da fdp da VA X, f(x).
curve(1.5 * (x ^ 2), -1, 1)
## Tem integral 1?
integrate(function(x) 1.5 * (x^2), lower = -1, upper = 1)# 1 with absolute error < 1.1e-14Vamos considerar como \(g\) (a distribuição proposta) a densidade de uma uniforme entre -1 e 1. Então se a base é 2, a altura deve ser 0.5 para ter produto 1, assim \(g(y) = 0.5, -1 < y < 1\). Qual deve ser um valor de \(M\) para garantir que \(f(x) \leq M g(x)\) para todo \(x\) dentro do intervalo \([-1, 1]\)? Pela definição acima, temos que: \[ M \geq \max_x \frac{f(x)}{g(x)} = \frac{1.5}{0.5} = 3 \] Portanto, fazemos \(M = 3\), pois esse é o valor mínimo necessário para satisfazer \(f(x) \leq M g(x)\) (e queremos o valor de \(M\) menor possível para mais eficiência computacional).
No gráfico abaixo, vemos a função \(f(x)\), a proposta \(g(x)\), e a que iremos de fato utilizar no algoritmo, a \(M g(x)\)
curve(1.5 * (x^2), -1, 1, col = 4)
curve(0.5 + 0 * x, add = TRUE, lty = 2)
curve(3 * 0.5 + 0 * x, add = TRUE, lty = 2, lwd = 2)
legend("bottomright", legend = c("f(x)", "g(x)", "M g(x)"),
lty = c(1, 2, 2), col = c(4, 1, 1), lwd = c(1, 1, 2), bty = "n")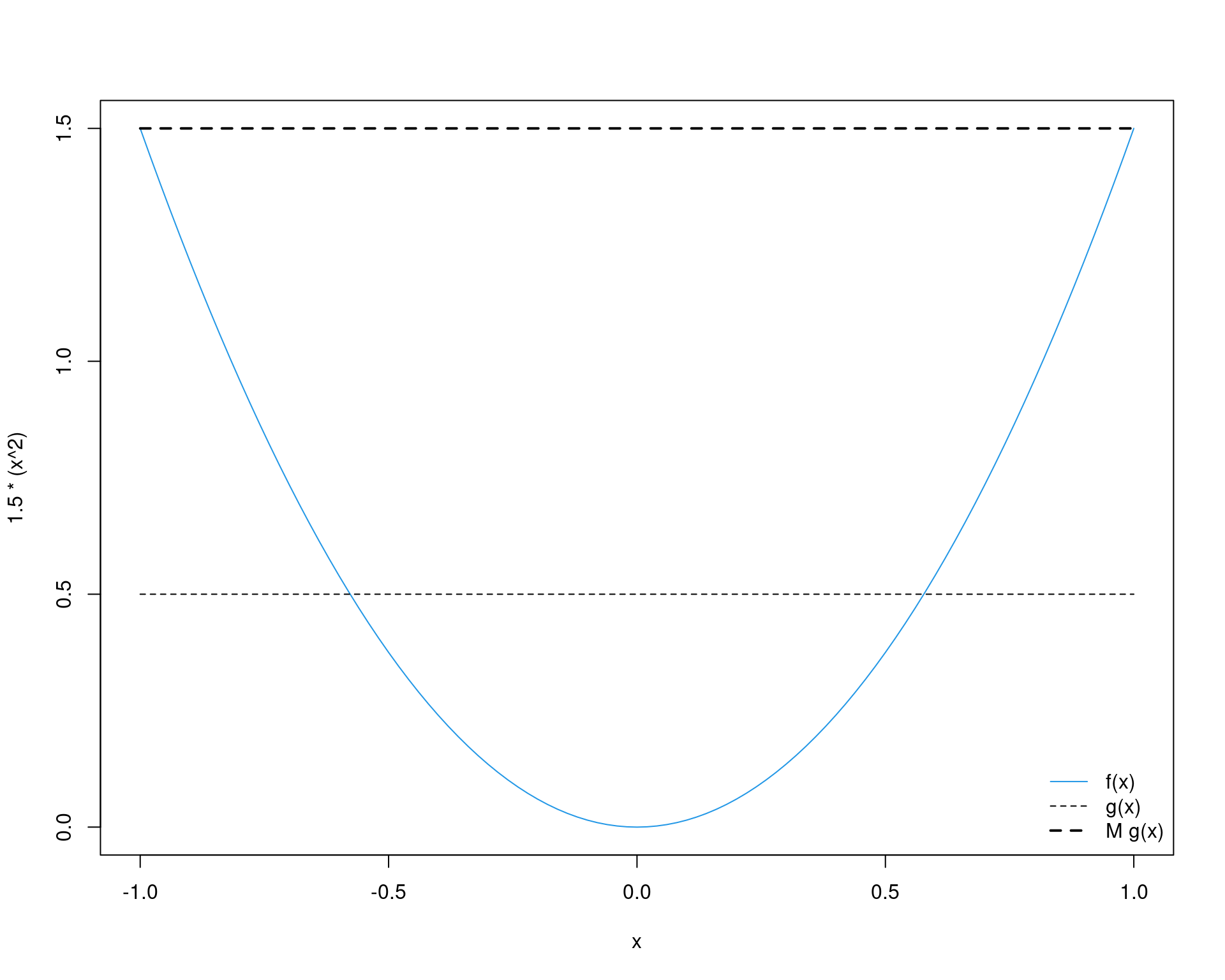
Agora podemos prosseguir com o algoritmo:
## Criando os elementos necessários.
f <- function(x) 1.5 * x^2
g <- function(x) 0.5 + 0 * x
M <- 3
x <- numeric(1)
## 1. Gerar y cuja densidade é g()
set.seed(1)
(y <- runif(n = 1, -1, 1))# [1] -0.4689827## 2. Gerar u de uma uniforme padrão.
(u <- runif(n = 1))# [1] 0.3721239## 3. Calcula a razão entre as densidades
(r <- f(y)/(M * g(y)))# [1] 0.2199447## 4. Compara e decide
if (u < r) {
x <- y
print("u < r então valor aceito.")
} else {
print("u >= r então valor descartado.")
}# [1] "u >= r então valor descartado."Verifica os pontos no gráfico:
curve(1.5 * (x^2), -1, 1, col = 4)
curve(3 * 0.5 + 0 * x, add = TRUE, lty = 2, lwd = 2)
legend("bottomright", legend = c("f(x)", "M g(x)"),
lty = c(1, 2), col = c(4, 1), lwd = c(1, 2), bty = "n")
points(y, 0, pch = 19, col = 5)
text(y, 0, bquote(y == .(round(y, 3))), pos = 4, col = 5)
points(y, f(y), pch = 19, col = 4)
text(y, f(y), bquote(f(y) == .(round(f(y), 3))), pos = 4, col = 4)
points(y, M * g(y), pch = 19, col = 1)
text(y, M * g(y), bquote(M %.% g(y) == .(M * g(y))), pos = 1, col = 1)
points(y, u * M * g(y), pch = 19, col = 2)
text(y, u * M * g(y), bquote(u == .(round(u, 3))), pos = 4, col = 2)
text(.15, 1, bquote(f(y) / M %.% g(y) == .(round(r, 3))), pos = 4)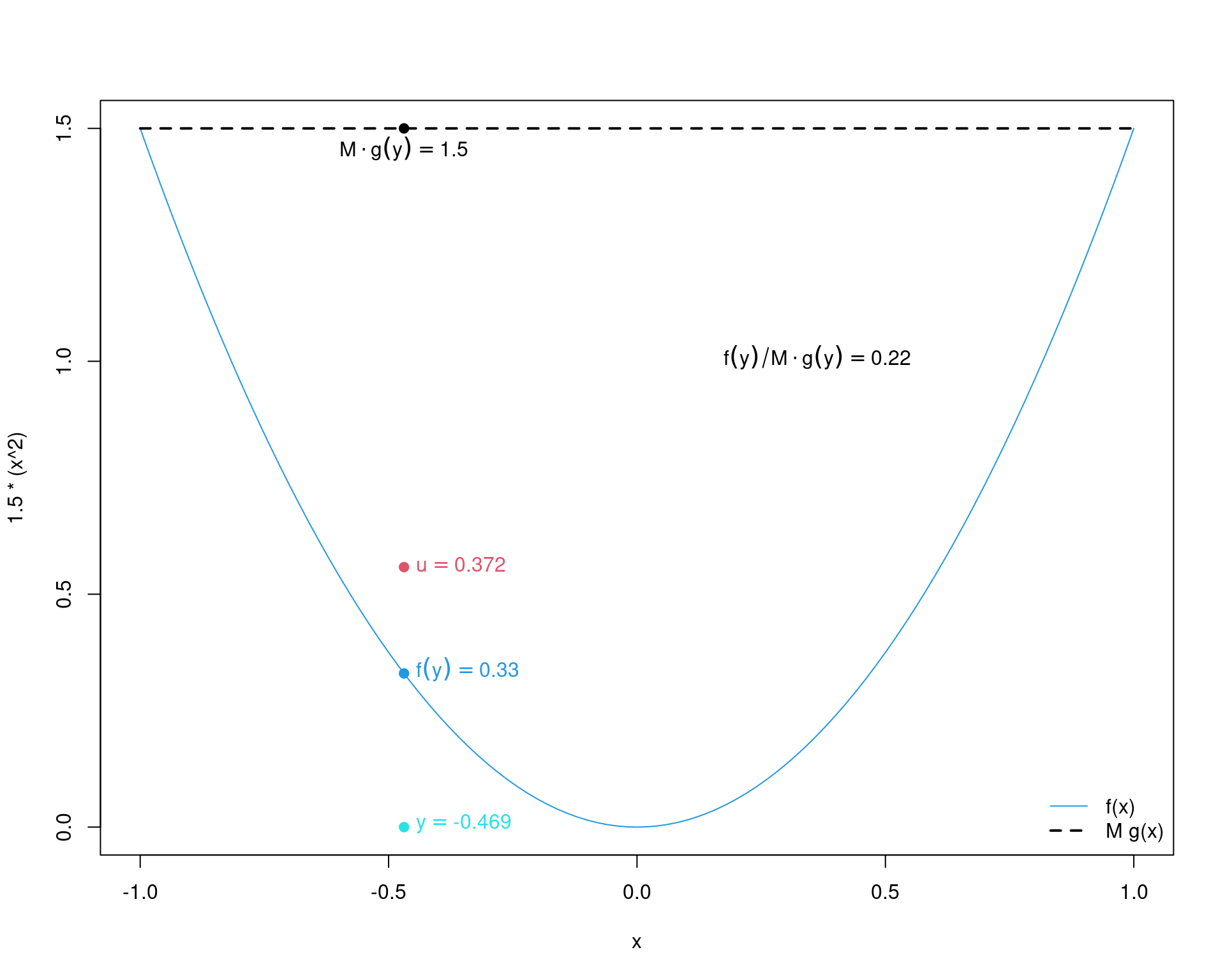
Note que o valor sorteado de \(y\) (da proposta \(\text{U}[-1,1]\)) foi -0.469. Os pontos azul e preto são as densidades da \(f\) e da \(g\) avaliadas nesse ponto. Como o valor sorteado \(u\) (da \(\text{U}[0,1]\)) foi \(0.372 > 0.22 = f(y)/Mg(y)\), então o valor de \(y\) é rejeitado. Isso fica claro pelo gráfico, pois esse ponto está em uma área acima da densidade de \(f\), portanto não deve fazer parte de uma amostra dessa distribuição.
Veja também que o valor de \(u\) é comparável com a razão \(f(y)/Mg(y)\), pois esta razão sempre será algum valor entre 0 e 1. Portanto o valor de \(u\) é sempre relativo à essa razão (i.e., não está na mesma escala das densidades de \(f\) e \(g\)).
Agora, podemos definir um algoritmo que repete esse processo para um número fixo de amostras da distribuição proposta.
## Simula de uma única vez, com um valor fixo de simulações
Nsim <- 2500
set.seed(1)
## Amostra da proposta
y <- runif(Nsim, -1, 1)
## Amostra da U(0,1)
u <- runif(Nsim)
## Calcula a razão
r <- f(y)/(M * g(y))
## x será um vetor com os valores de y onde u < r
x <- y[u < r]
## Valores de u aceitos (apenas para o grafico)
ua <- u[u < r]
## Valores de u rejeitados (apenas para o grafico)
ur <- u[u >= r]Graficamente, temos a seguinte situação. Os pontos verde são aqueles aceitados na simulação, e portanto, farão parte da amostra aleatória da distribuição \(f\) que queremos. Os pontos em vermelho são todos aqueles que foram rejeitados e foram descartados.
curve(1.5 * (x^2), -1, 1, col = 4)
curve(3 * 0.5 + 0 * x, add = TRUE, lty = 2, lwd = 2)
points(x, ua * M * g(x), col = 3)
points(y[u >= r], ur * M * g(y[u >= r]), col = 2)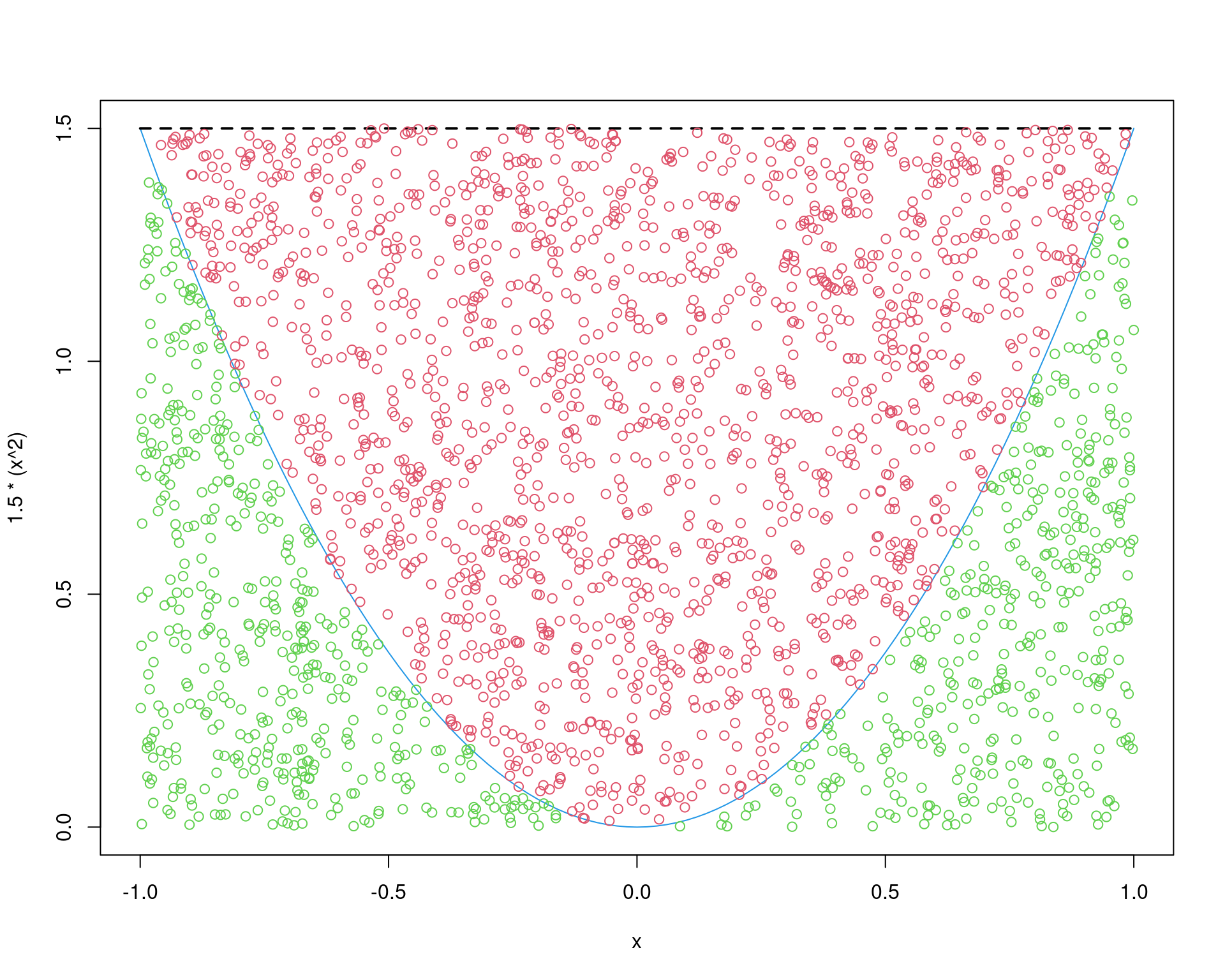
Lembre-se que a taxa teórica de aceitação é \(1/M\), portanto, podemos conferir isso com essa amostra específica.
## Quantos foram aceitados
length(x)/length(y)# [1] 0.3456## Taxa (teorica) de aceitacao é
1/M# [1] 0.3333333## Quantos foram rejeitados
length(ur)/length(u)# [1] 0.6544No algoritmo acima, fixamos o número de amostras de \(g\) (2500), e com isso, obtivemos uma
amostra de apenas 864 valores de \(f\)
(porque a taxa de aceitação foi de 35%). No entanto, na maioria das
vezes, o que queremos é gerar um número fixo \(N\) de valores da distribuição de interesse
\(f\). Como não temos como prever
antecipadamente a taxa de aceitação para cada simulação, então
precisamos de uma estrutura de repetição como o while(),
que executará o algoritmo o número de vezes necessário para gerar uma
amostra com exatamente \(N\)
valores.
## Simula 1000 valores de f
N <- 1000L
x <- numeric(0)
while(length(x) < N) {
y <- runif(1, -1, 1)
u <- runif(1)
r <- f(y)/(M * g(y))
if(u < r) {
## Não é a forma mais eficiente!
x <- c(x, y)
}
}
length(x)# [1] 1000Podemos então verificar se a simulação gerou de fato valores de \(f\) através de um histograma e da comparação das distribuições acumuladas da amostra (empírica) e teórica (definido a expressão analítica para a acumulada \(F_X(x)\)).
par(mfrow = c(1, 2))
hist(x)
Fx <- function(x) 0.5 * (x^3 + 1)
plot(ecdf(x))
curve(Fx, add = TRUE, from = -1, to = 1, col = 2)
legend("right", legend = c("Empírica", "Teórica"),
lty = 1, col = 1:2, bty = "n")
par(mfrow = c(1, 1))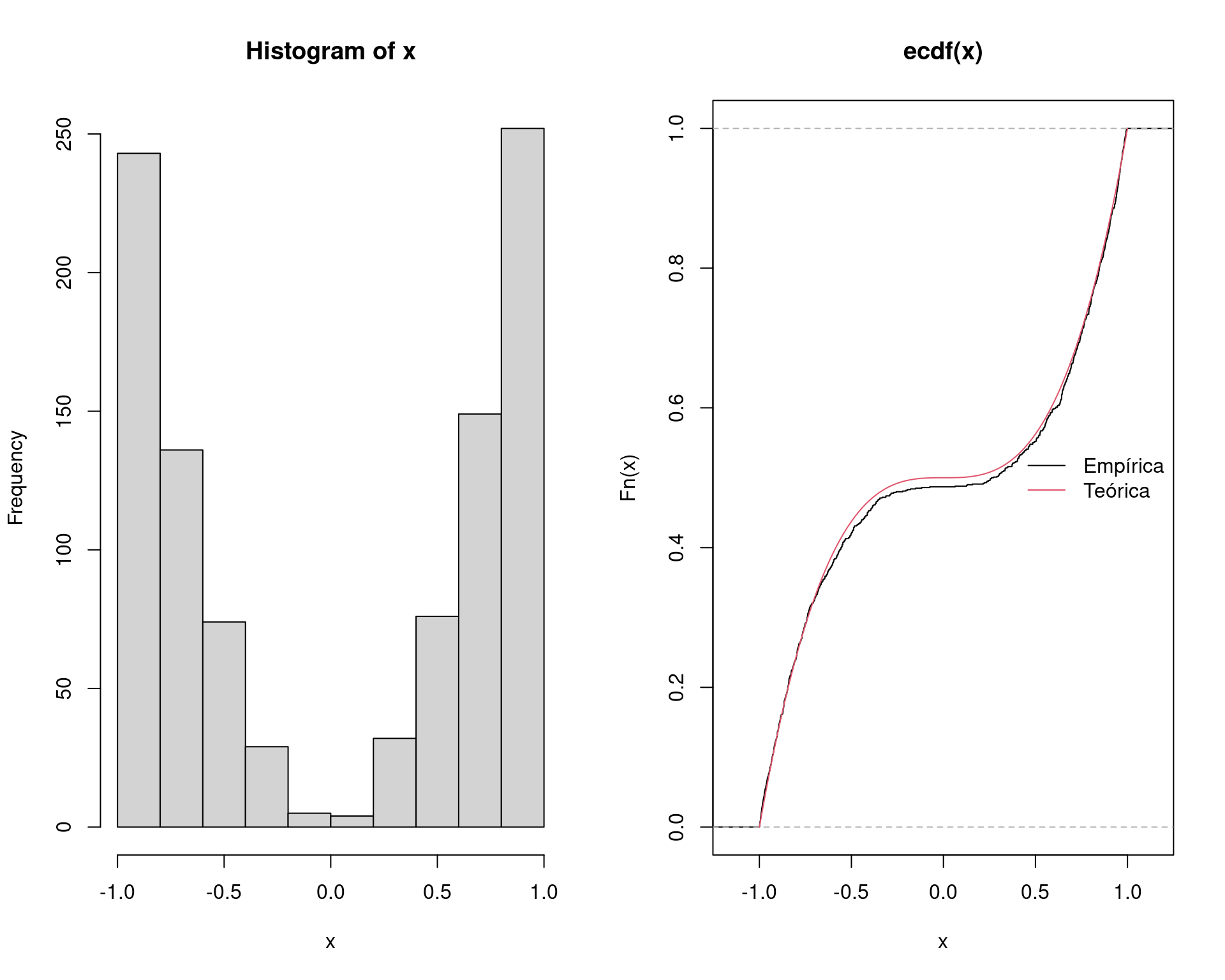
2.2 Exemplo 2
Considere que deseja-se gerar valores de uma distribuição \(\text{Beta}(\alpha = 2.7, \beta = 6.3)\) (e
também suponha que não dispomos de um gerador como o que já existe no R
pela função rbeta()).
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1)
A distribuição proposta mais natural seria uma Uniforme entre 0 e 1, que possui densidade 1 (para todo \(x\)).
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1, col = 4)
curve(1 + 0 * x, from = 0, to = 1, add = TRUE, lty = 2)
legend("topright", legend = c("f(x)", "g(x)"),
lty = c(1, 2), col = c(4, 1), bty = "n")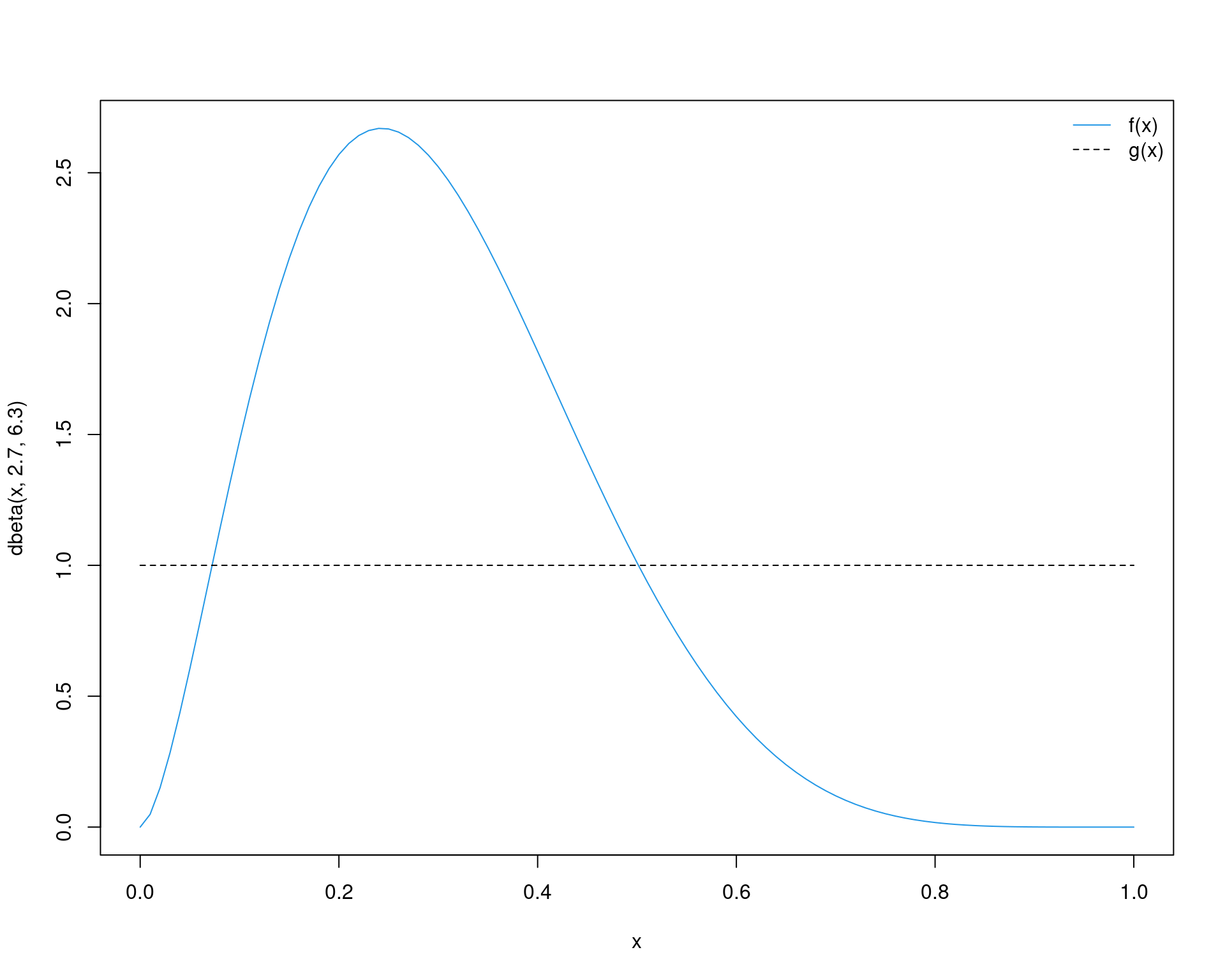
Como podemos achar o valor de \(M\) que satisfaça \(f(x) \leq M g(x)\)? Já vimos que esse valor pode ser determinado por \[ M \geq \max_x \frac{f(x)}{g(x)} \] O valor máximo da densidade de \(g(x)\) é fácil de ser encontrado, pois nesse caso é 1 para todo \(x\). Como fazer então para determinar o valor máximo da \(\text{Beta}(2.7, 6.3)\)? Temos duas opções:
- Usar a expressão da moda da distribuição (se existir)
- Achar esse valor máximo por otimização numérica
No caso da distribuição Beta, existe uma expressão fechada para de determinar a moda, que é \(\frac{\alpha-1}{\alpha+\beta-2}\). Portanto seria fácil nesse caso determinar o valor máximo da densidade por meio de
## Define parâmetros
alfa <- 2.7; beta <- 6.3
## A moda é
(moda <- (alfa - 1)/(alfa + beta - 2))# [1] 0.2428571## A densidade nesse ponto é então
dbeta(moda, alfa, beta)# [1] 2.669744No entanto, em diversas situações, não temos uma expressão fechada para a moda ou ela não pode ser determinada analiticamente. Por isso, nesses casos, podemos encontrar o valor máximo da função através de otimização numérica dessa função. Esse método serve para qualquer distribuição (na verdade qualquer função) onde deseja-se obter o ponto de máxima.
No R, podemos passar a função que desejamos maximizar para a função
optimize(). Aqui usaremos a função dbeta() que
já implementa a expressão de densidade da Beta, mas poderíamos também
escrever essa função manualmente e usá-la na otimização.
(max.beta <- optimize(f = function(x) {dbeta(x, alfa, beta)},
interval = c(0, 1), maximum = TRUE))# $maximum
# [1] 0.2428608
#
# $objective
# [1] 2.669744Note que a função retorna dois valores: o ponto onde foi encontrada a densidade máxima (igual a moda), e o valor da densidade nesse ponto. Veja que os resultados são virtualmente os mesmos dos anteriores obtidos de forma analítica. Por ser uma forma mais geral, prosseguiremos com o valor de densidade máximo obtido dessa forma. Agora podemos então determinar o valor de \(M\), como sendo
(M <- max.beta$objective/1)# [1] 2.669744Assim, ficamos com a distribuição proposta \(Mg(x)\) como pode ser visto abaixo.
curve(dbeta(x, alfa, beta), from = 0, to = 1, col = 4)
curve(1 + 0 * x, from = 0, to = 1, add = TRUE, lty = 2)
curve(M * 1 + 0 * x, add = TRUE, lty = 2, lwd = 2)
legend("right", legend = c("f(x)", "g(x)", "M g(x)"),
lty = c(1, 2, 2), col = c(4, 1, 1), lwd = c(1, 1, 2), bty = "n")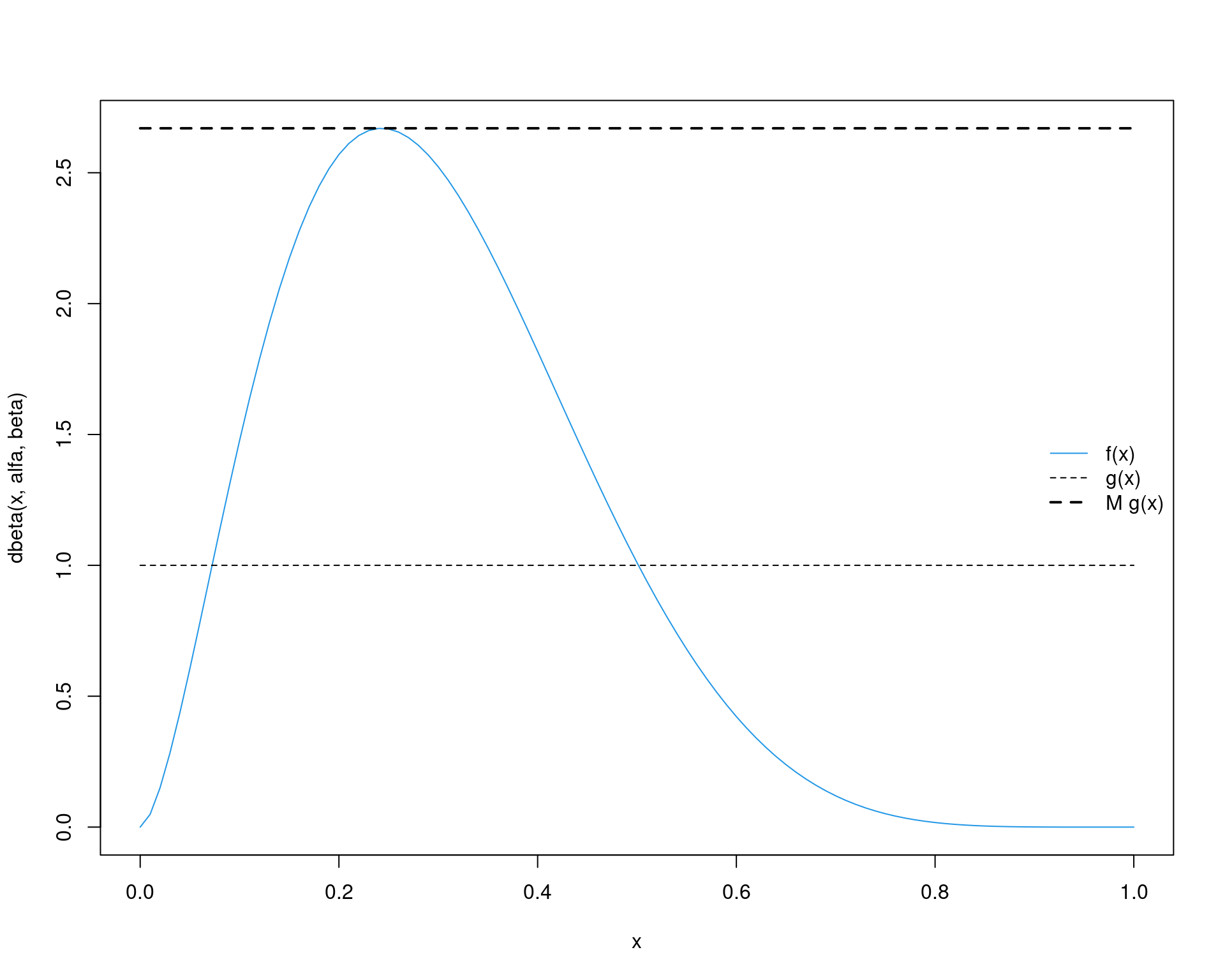
Seguindo com o algoritmo de aceitação e rejeição, a ideia é a mesma do exemplo anterior, mudando as funções apropriadamente.
## Define funções
f <- function(x) dbeta(x, alfa, beta)
g <- function(x) 1 + 0 * x
## Simula com número fixo
Nsim <- 2500
## Amostra da proposta U(0,1)
y <- runif(Nsim)
## Amostra u também de U(0,1)
u <- runif(Nsim)
## Calcula a razão
r <- f(y)/(M * g(y))
## x serão os valores de y onde u < r
x <- y[u < r]
## Aceitados
ua <- u[u < r]
## Rejeitados
ur <- u[u >= r]Assim como no exemplo anterior, podemos visualizar os pontos amostrados que foram aceitados e aqueles rejeitados.
curve(dbeta(x, alfa, beta), from = 0, to = 1, col = 4)
curve(M * 1 + 0 * x, from = 0, to = 1, add = TRUE, lty = 2, lwd = 2)
points(x, ua * M * g(x), col = 3)
points(y[u >= r], ur * M * g(y[u >= r]), col = 2)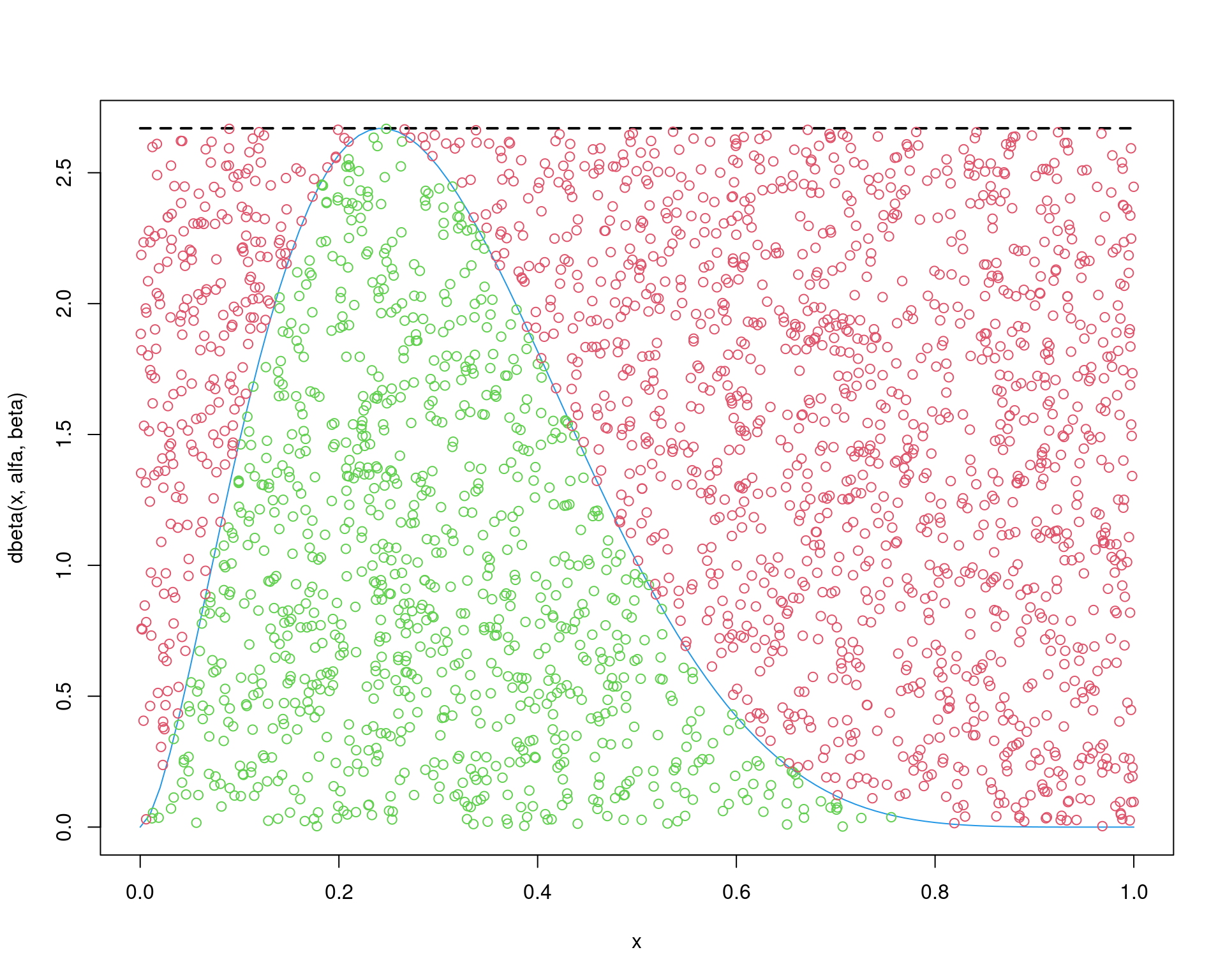
Lembre-se que a taxa de aceitação teórica é \(1/M\), e neste exemplo temos
## Quantos foram aceitados
length(x)/length(y)# [1] 0.3768## Taxa (teorica) de aceitacao é
1/M# [1] 0.3745677Note pelo gráfico acima que a maior parte dos pontos amostrados não são aceitos (veja também a baixa taxa de aceitação). Isso mostra que estamos desperdiçando a maior parte do tempo computacional amostrando pontos que não serão aceitos.
Devemos então pensar em uma outra distribuição proposta, com a intenção de melhorar (aumentar) a taxa de aceitação. Naturalmente, uma distribuição proposta com um formato mais próximo daquele que queremos amostrar seria possivelmente mais eficiente.
Considere então como uma nova distribuição proposta uma \(\text{Beta}(2, 6)\) (ainda queremos amostrar de uma \(\text{Beta}(2.7, 6.3)\)).
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1, col = 4, ylim = c(0, 3))
curve(dbeta(x, 2, 6), from = 0, to = 1, add = TRUE, lty = 2)
legend("topright", legend = c("f(x)", "g(x)"),
lty = c(1, 2), col = c(4, 1), bty = "n")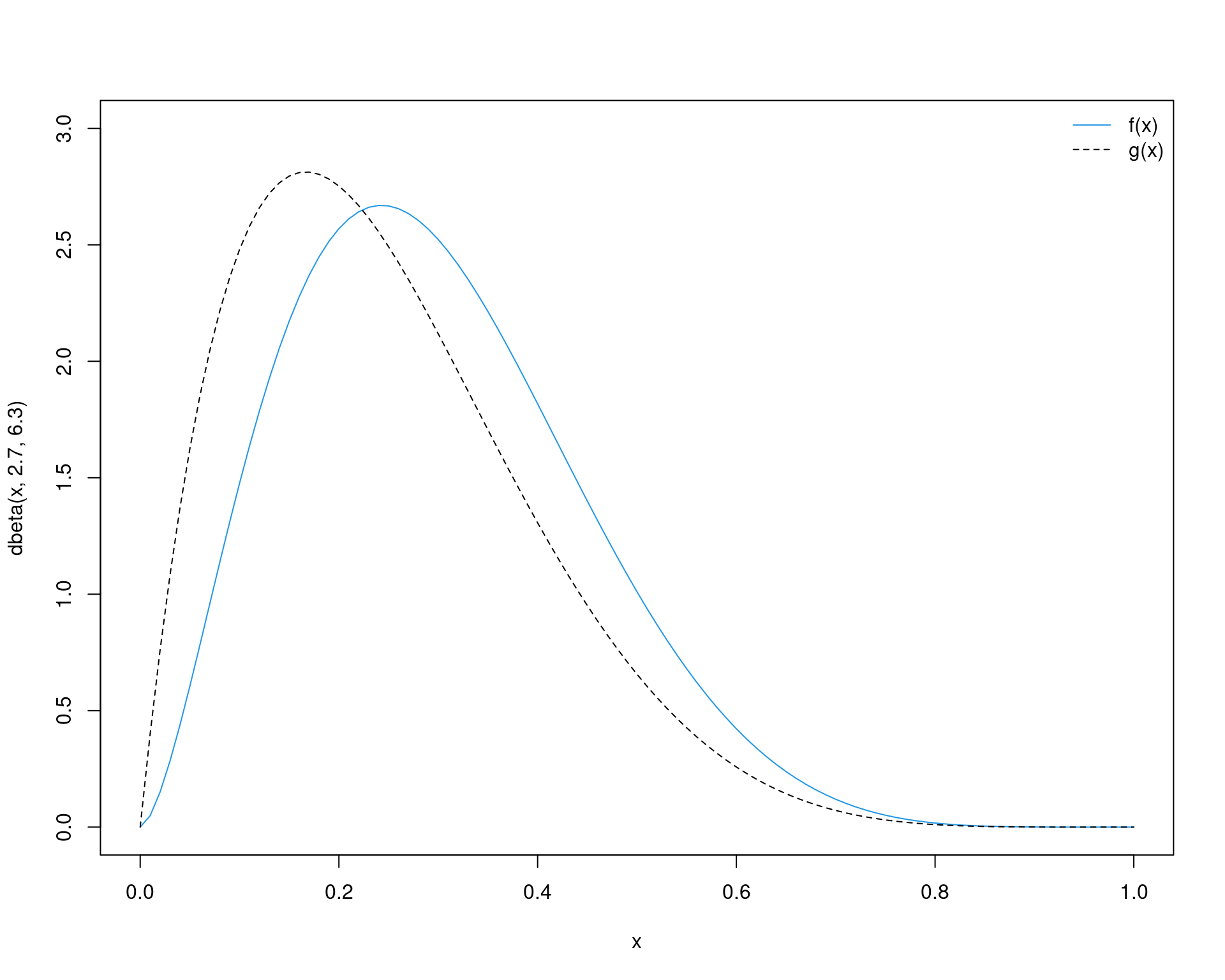
Com o formato mais próximo da proposta, certamente a taxa de aceitação será maior. Precisamos novamente encontrar o valor \(M\) que satisfaça \(f(x) \leq M g(x)\). Já vimos que podemos usar a moda, mas vamos usar o método geral de encontrar a densidade máxima das duas distribuições por otimização numérica. Aqui também temos duas opções:
- Encontrar o máximo de cada função separadamente e fazer a razão entre eles
- Encontrar diretamente o máxima da razão entre as duas distribuições
A segunda abordagem é mais direta e levará ao mesmo resultado da primeira, mas só precisaremos fazer uma otimização. Portanto prosseguimos com
(M <- optimize(f = function(x) {dbeta(x, 2.7, 6.3)/dbeta(x, 2, 6)},
interval = c(0, 1), maximum = TRUE)$objective)# [1] 1.671808Note que esse já é o valor de \(M\), e ficamos com a seguinte situação
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1, col = 4, ylim = c(0, 5))
curve(dbeta(x, 2, 6), from = 0, to = 1, add = TRUE, lty = 2)
curve(M * dbeta(x, 2, 6), add = TRUE, lty = 2, lwd = 2)
legend("topright", legend = c("f(x)", "g(x)", "M g(x)"),
lty = c(1, 2, 2), col = c(4, 1, 1), lwd = c(1, 1, 2), bty = "n")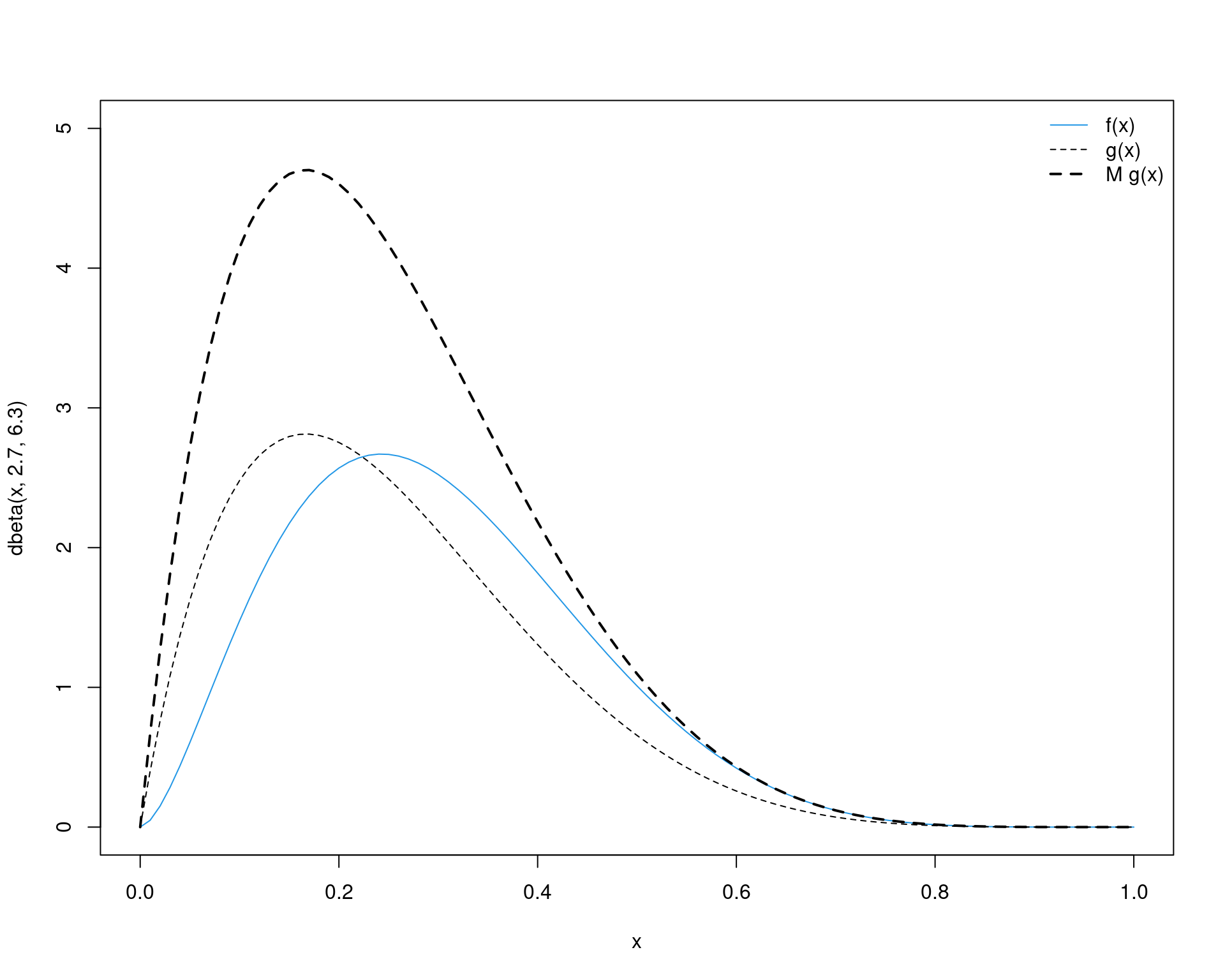
Agora fazemos o mesmo processo para um número fixo de simulações
## Define funções
f <- function(x) dbeta(x, 2.7, 6.3)
g <- function(x) dbeta(x, 2, 6)
## Simula
Nsim <- 2500
## Amostra da proposta
y <- rbeta(Nsim, 2, 6)
## Amostra da U(0,1)
u <- runif(Nsim)
r <- f(y)/(M * g(y))
x <- y[u < r]
ua <- u[u < r]
ur <- u[u >= r]O resultado dos pontos aceitados agora pode ser visto abaixo.
curve(dbeta(x, 2.7, 6.3), from = 0, to = 1, col = 4, ylim = c(0, 5))
curve(M * dbeta(x, 2, 6), from = 0, to = 1, add = TRUE, lty = 2, lwd = 2)
points(x, ua * M * g(x), col = 3)
points(y[u >= r], ur * M * g(y[u >= r]), col = 2)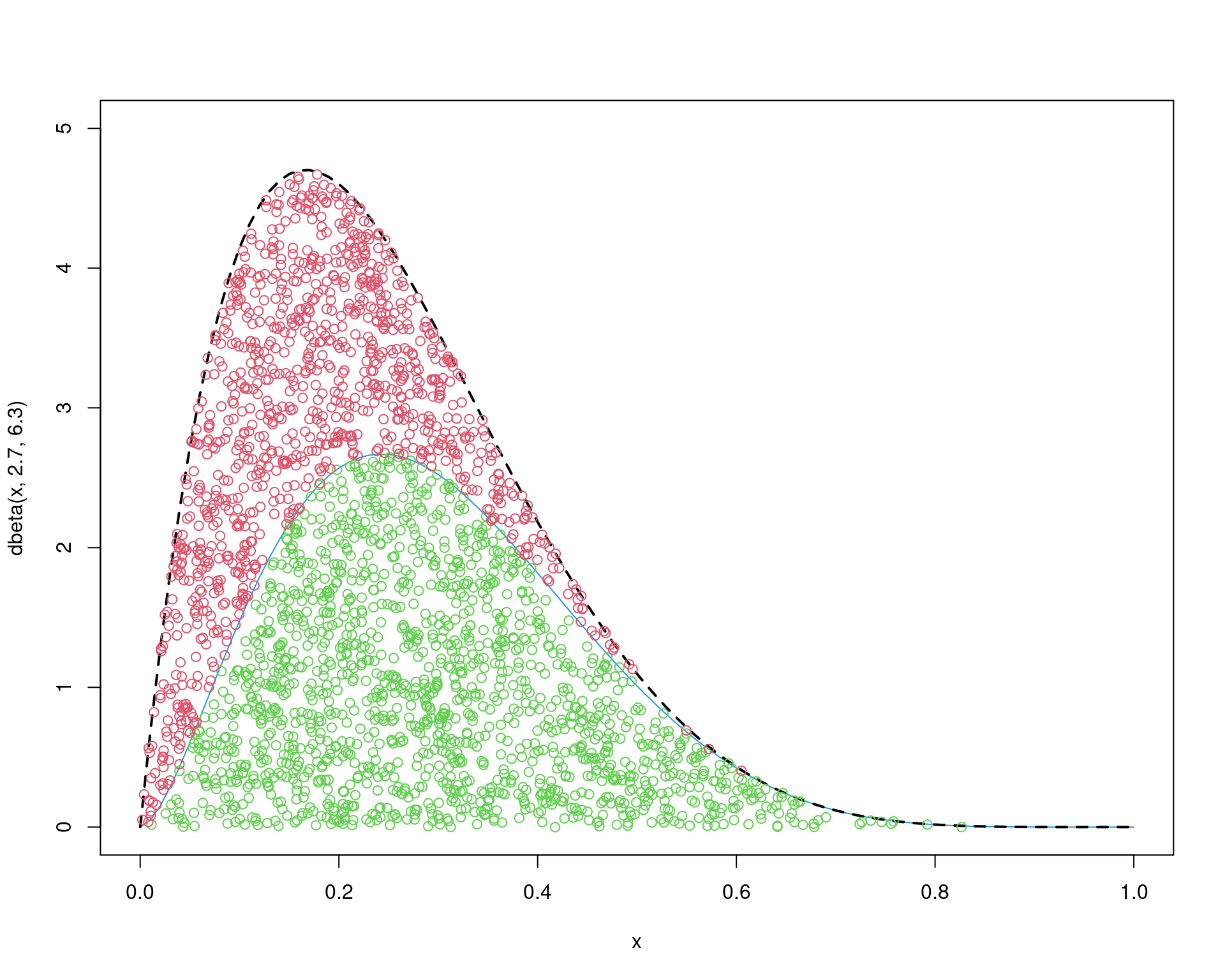
Veja que muitos mais pontos agora são aceitos. De fato, a taxa de aceitação usando essa nova distribuição proposta é bem maior quando comparada à taxa anterior com a uniforme como proposta.
## Quantos foram aceitados
length(x)/length(y)# [1] 0.5988## Taxa (teorica) de aceitacao é
1/M# [1] 0.5981549Novamente, podemos verificar a distribuição da amostra gerada através de um histograma, e (preferencialmente), através das distribuições acumuladas empírica e teórica.
par(mfrow = c(1, 2))
hist(x, freq = FALSE); lines(density(x), col = 2)
plot(ecdf(x))
curve(pbeta(x, 2.7, 6.3), add = TRUE, from = 0, to = 1, col = 2)
legend("right", legend = c("Empírica", "Teórica"),
lty = 1, col = 1:2, bty = "n")
par(mfrow = c(1, 1))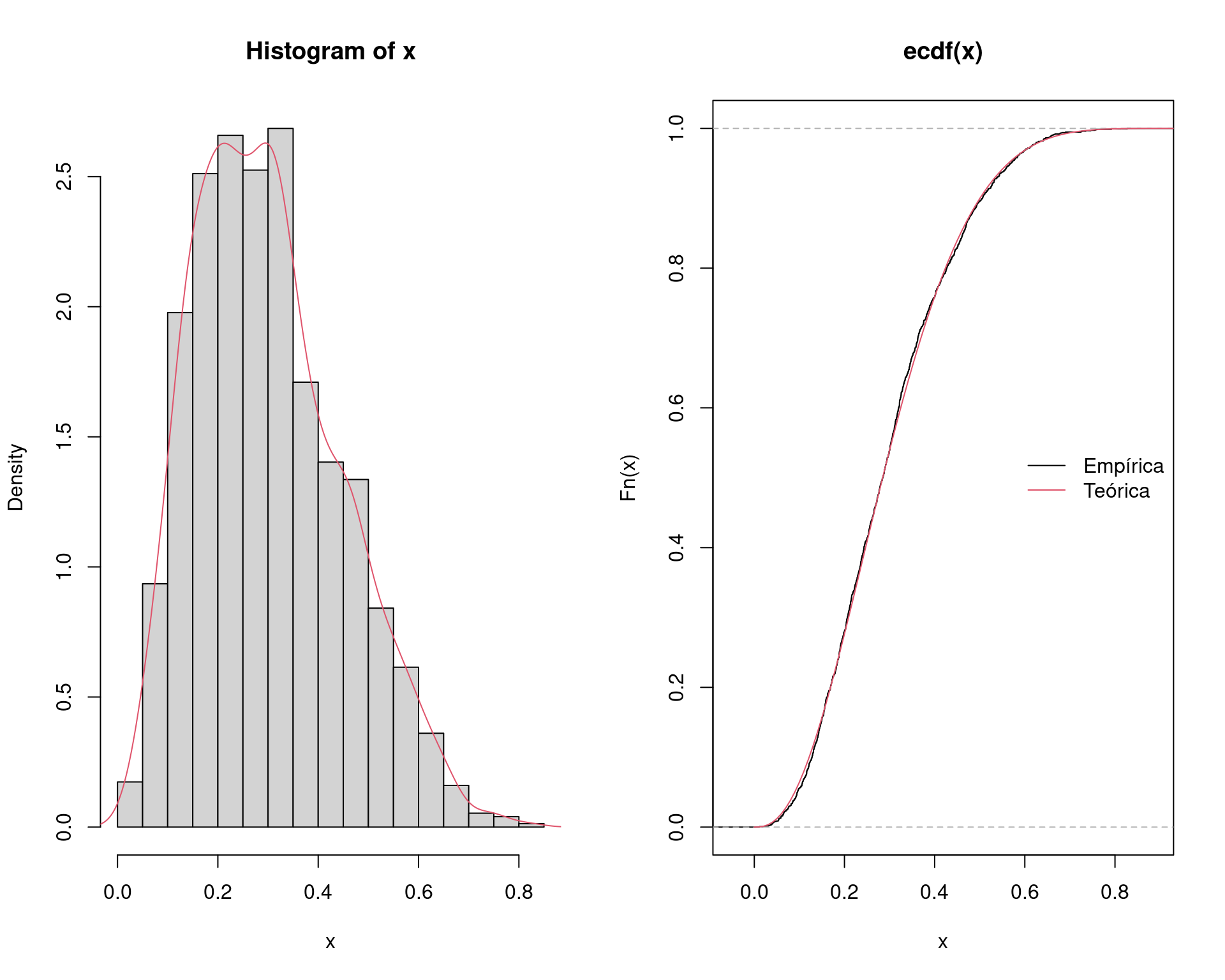
2.3 Exemplo 3
Suponha que deseja-se gerar valores de uma VA \(X \sim \text{N}(0, 1)\) a partir de uma VA \(Y \sim \text{Cauchy}(0, 1)\).
## Verifica as distribuições
curve(dnorm(x), -6, 6)
curve(dcauchy(x), add = TRUE, lty = 2)
legend("topright", legend = c("Normal", "Cauchy"),
lty = c(1, 2))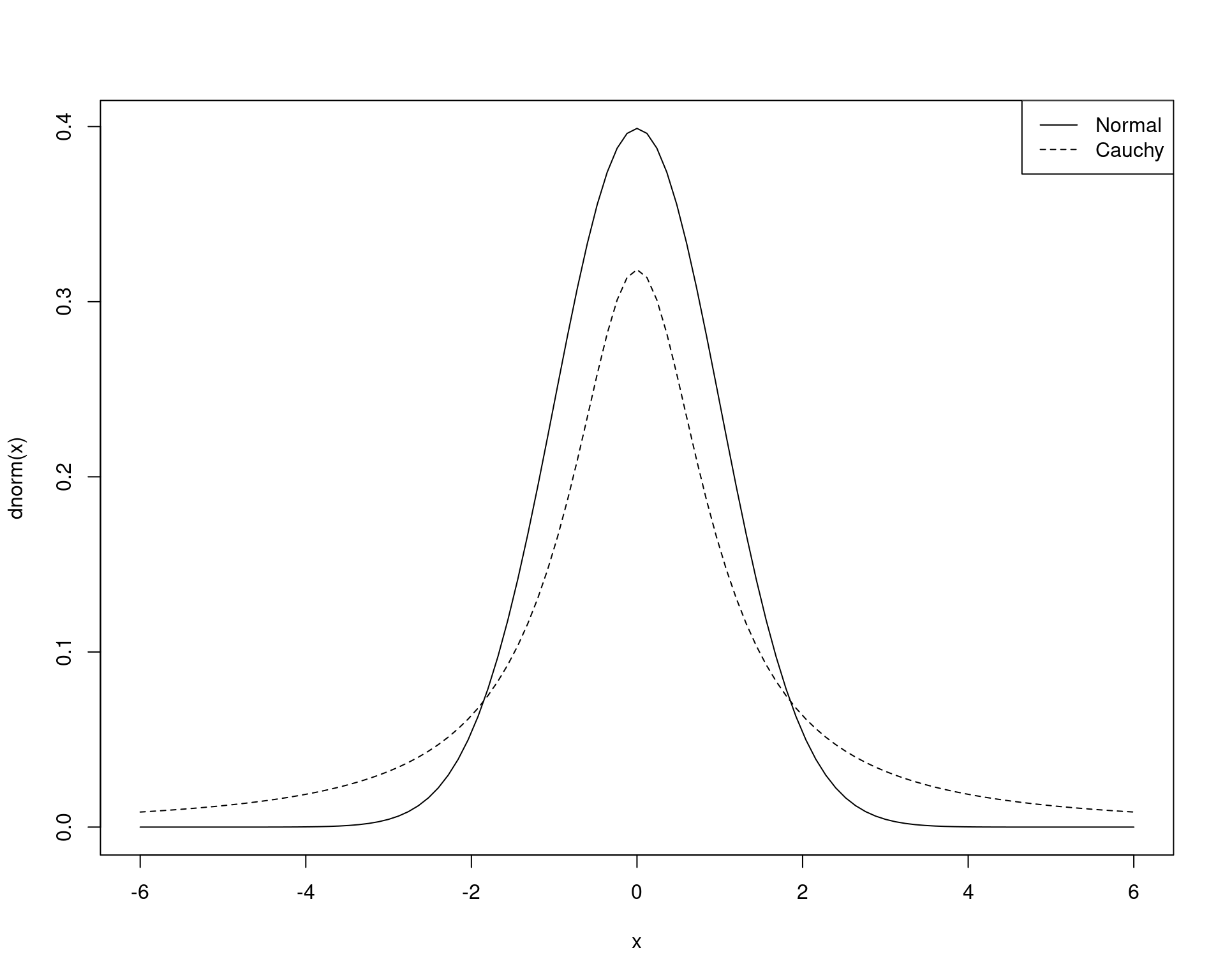
## Obtém valor de M por otimização
(M <- optimize(f = function(x) {dnorm(x)/dcauchy(x)},
interval = c(-6, 6), maximum = TRUE)$objective)# [1] 1.520347## Verifica as relações
curve(M * dcauchy(x), lty = 2, lwd = 2, -6, 6,
ylim = c(0, M * dcauchy(0)))
curve(dnorm(x), add = TRUE)
curve(dcauchy(x), add = TRUE, lty = 2)
legend("topright", legend = c("f(x)", "g(x)", "M g(x)"),
lty = c(1, 2, 2), lwd = c(1, 1, 2), bty = "n")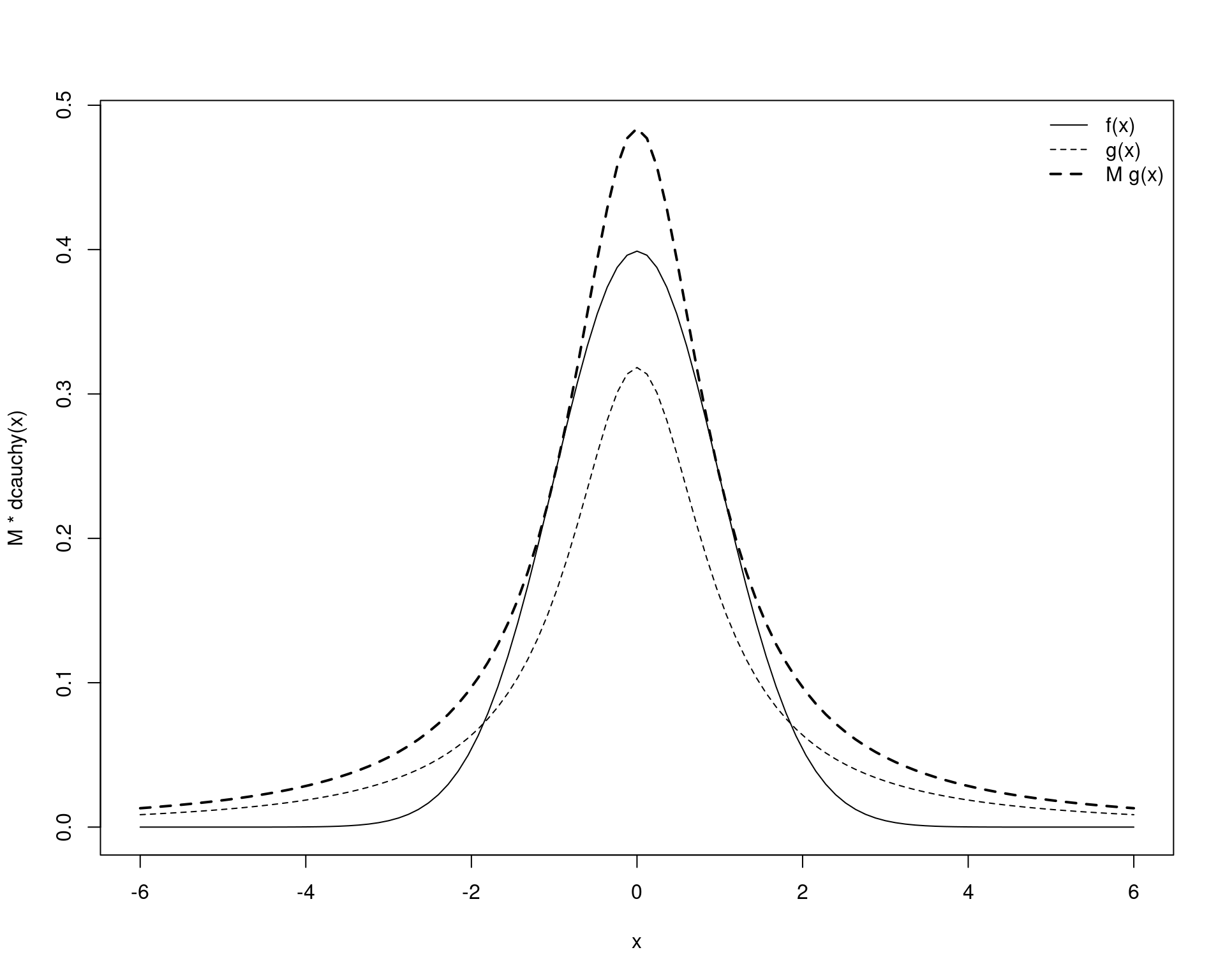
## Cria as funções
f <- function(x) dnorm(x, 0, 1)
g <- function(x) dcauchy(x, 0, 1)
## Simula
Nsim <- 2500
## Amostra da proposta
y <- rcauchy(Nsim)
## Amostra da U(0,1)
u <- runif(Nsim)
r <- f(y)/(M * g(y))
x <- y[u < r]
ua <- u[u < r]
ur <- u[u >= r]
## Gráfico de aceitação
curve(dnorm(x), from = -6, to = 6, col = 4, ylim = c(0, .5))
curve(M * dcauchy(x), add = TRUE, lty = 2, lwd = 2)
points(x, ua * M * g(x), col = 3)
points(y[u >= r], ur * M * g(y[u >= r]), col = 2)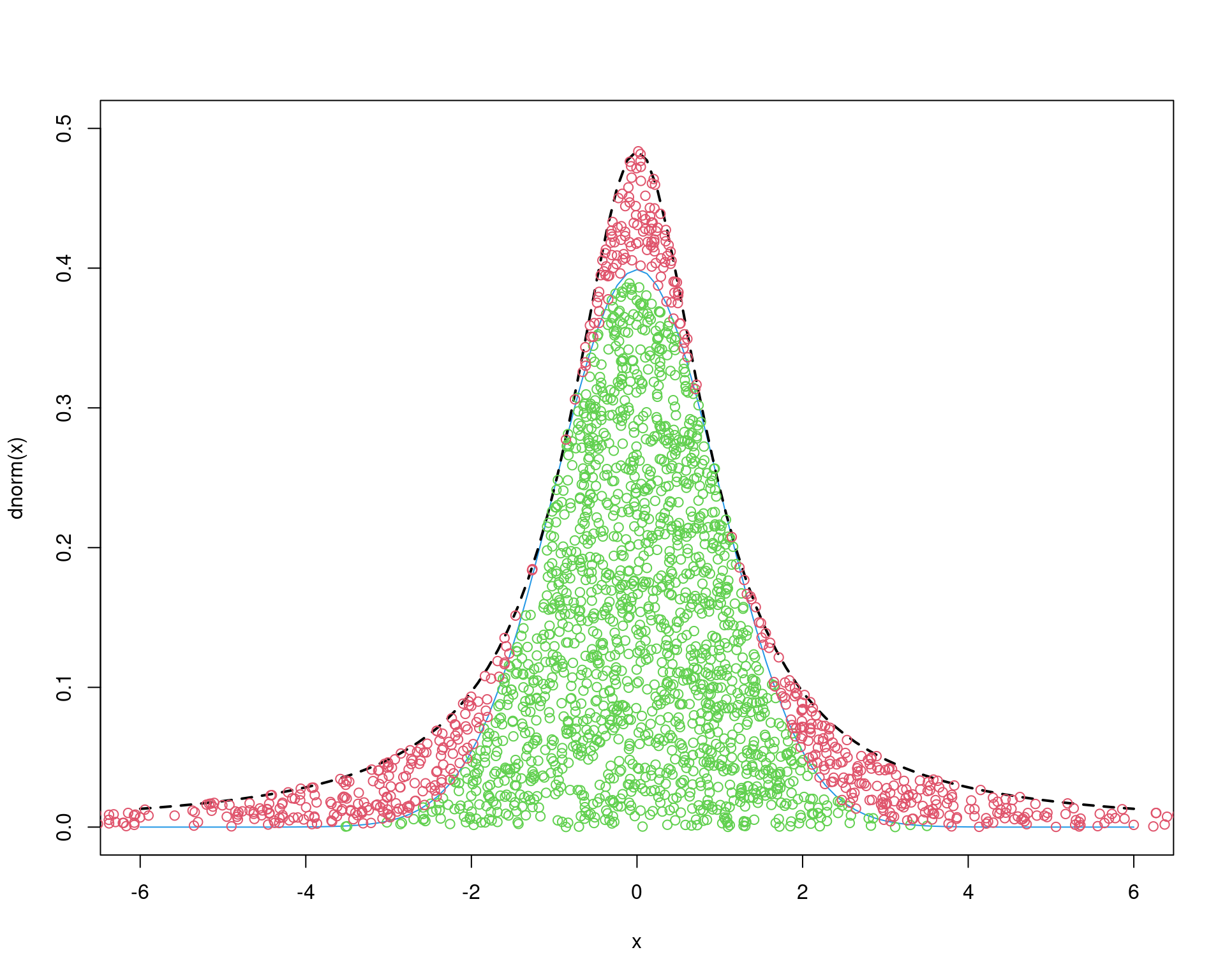
##----------------------------------------------------------------------
## Aplicação direta do método para N valores
n <- 1 # Contador de valores aceitos
l <- 1 # Contador de ciclos
N <- 1000 # Total de número à gerar
x <- numeric(N)
while (n < N) {
y <- rcauchy(1)
u <- runif(1)
r <- f(y)/(M * g(y))
if (u < r) {
x[n] <- y
n <- n + 1
}
l <- l + 1
}
## Verifica distribuição
par(mfrow = c(1, 2))
hist(x)
plot(ecdf(x))
curve(pnorm(x), add = TRUE, col = 2)
legend("right", legend = c("Empírica", "Teórica"),
lty = 1, col = 1:2, bty = "n")
par(mfrow = c(1, 1))
## Taxa de aceitação observada
n/l# [1] 0.6459948## Taxa de aceitação teórica
1/M# [1] 0.6577446Para uma ilustração animada veja este exemplo
3 Exercícios
- A partir do algoritmo que simula 1000 valores da distribuição do
exemplo 1, proponha um código mais eficiente (i.e. que não cresça o
vetor
xcomo feito lá). - Para a distribuição Beta do exemplo 2, escreva um algoritmo geral que gere um número fixo \(N\) de valores.
Este conteúdo está disponível por meio da Licença Creative Commons 4.0
