Métodos de reamostragem

Bootstrap (não paramétrico)

1 Introdução

• Os métodos de Bootstrap são uma classe de métodos de Monte Carlo não paramétricos, que estimam a distribuição de uma população por reamostragem
• Métodos de reamostragem tratam a amostra observada como uma população finita
  • A distribuição da população finita representada pela amostra observada, pode ser entendida como uma pseudo-população, com características similares às da população original
• Amostra aleatórias são geradas (reamostragem) a partir da amostra original, para estimar características populacionais e fazer inferência sobre a população amostrada
  • Através da reamostragem, a distribuição amostral de uma estatística pode ser estimada, e as propriedades de um estimador podem então ser calculadas através do erro padrão e cálculos de viés
• Métodos de bootstrap são utilizados quando a distribuição da população alvo não é especificada (ou conhecida), e a amostra é a única informação disponível.

\[ \begin{aligned} &F \rightarrow X \rightarrow F_n \\ &F_n \rightarrow X^{\star} \rightarrow F_n^{\star} \end{aligned} \]

Justificativas

• Métodos computacionalmente intensivos para inferência estatística são usados quando as abordagens tradicionais não são adequadas.
• Resultados assintóticos em pequenas amostras.
• Violação de pressupostos.
• Não existência de mecanísmos de inferência específicos.
• Tais métodos se baseiam em reamostragem e/ou simulação.
• Podem ser aplicados em muitos contextos.

Bootstrap: visão geral

• Boostrap foi apresentado de forma sistematizada por Efron (1979).
• O termo bootstrap foi usado por Efron (1979) com o mesmo espírito que Tukey (1958) usou Jackknife (canivete suiço)
• O método já havia sido usado em circustâncias anteriores.
• Bootstrap é um método de reamostragem que pode usado para avaliar propriedades de estimadores e fazer inferência.
• Bootstrap é um método de Monte Carlo pois usa a distribuição empírica dos dados como se fosse a verdadeira distribuição.
• Principais aplicações de bootstrap:
  • Avaliar propriedades da distribuição de estimadores para seleção, ajuste de vício, etc.
  • Substituir ou aprimorar a adequação de abordagens assintóticas em amostras pequenas: intervalos de confiança, testes de hipótese.

Funcionamento

• Considere uma amostra de observações iid \(x_i\), \(i = 1, \ldots, n\)
• Usando a distribuição empírica, cada valor \(x_i\) tem igual probabilidade \(1/n\) de ocorrer.
• Considere que \(\theta\) seja um parâmetro de interesse que dispõe de um estimador \(\hat{\theta} = f(X_1, ..., X_n)\).
• Uma amostra bootstrap é um conjunto de valores extraídos ao acaso com reposição da amostra original.
• A estimativa de \(\theta\) na \(b\)-ésima reamostra bootstrap é \(\hat{\theta}^{b}\).

Algoritmo

Para cada estimativa de bootstrap indexada \(b = 1, \ldots, B\):

1. Gere uma amostra \(x^{\star} = (x_1^{\star}, \ldots, x_n^{\star})\), através de amostragem com reposição de amostra observada \(x_1, \ldots, x_n\)
2. Calcule a \(b\)-ésima estimativa \(\hat{\theta}^{(b)}\) da \(b\)-ésima amostra de bootstrap

O valor médio bootstrap é \[ \overline{\hat{\theta}^\star} = \frac{1}{B} \sum_{b = 1}^{B} \hat{\theta}^{(b)}. \] Entretanto, de forma geral não se recomenda esta valor para estimar \(\theta\). O bootstrap fornece boas aproximações para a forma e amplitude da distribuição amostral mas não necessariamente para a sua locação. O valor médio bootstrap é utilizado para avaliar e corrigir um possível viés do estimador, o que será discutido mais aditnate. Mas antes, vejamos um exemplo.

Exemplo da aula anterior

## Exemplo adaptado de Manly (1997)
## Comparação do comprimento da mandíbula de chacais machos e fêmeas
set.seed(2)
machos <- c(120, 107, 110, 116, 114, 111, 113, 117, 114, 112)
## Simula diferença para as femeas
femeas <- rnorm(10, mean(machos) - 2, sd = sd(machos))
da <- data.frame(comp = c(machos, femeas),
                 sexo = c(rep("M", 10), rep("F", 10)))
lattice::densityplot(~comp, groups = sexo, data = da, auto.key = TRUE)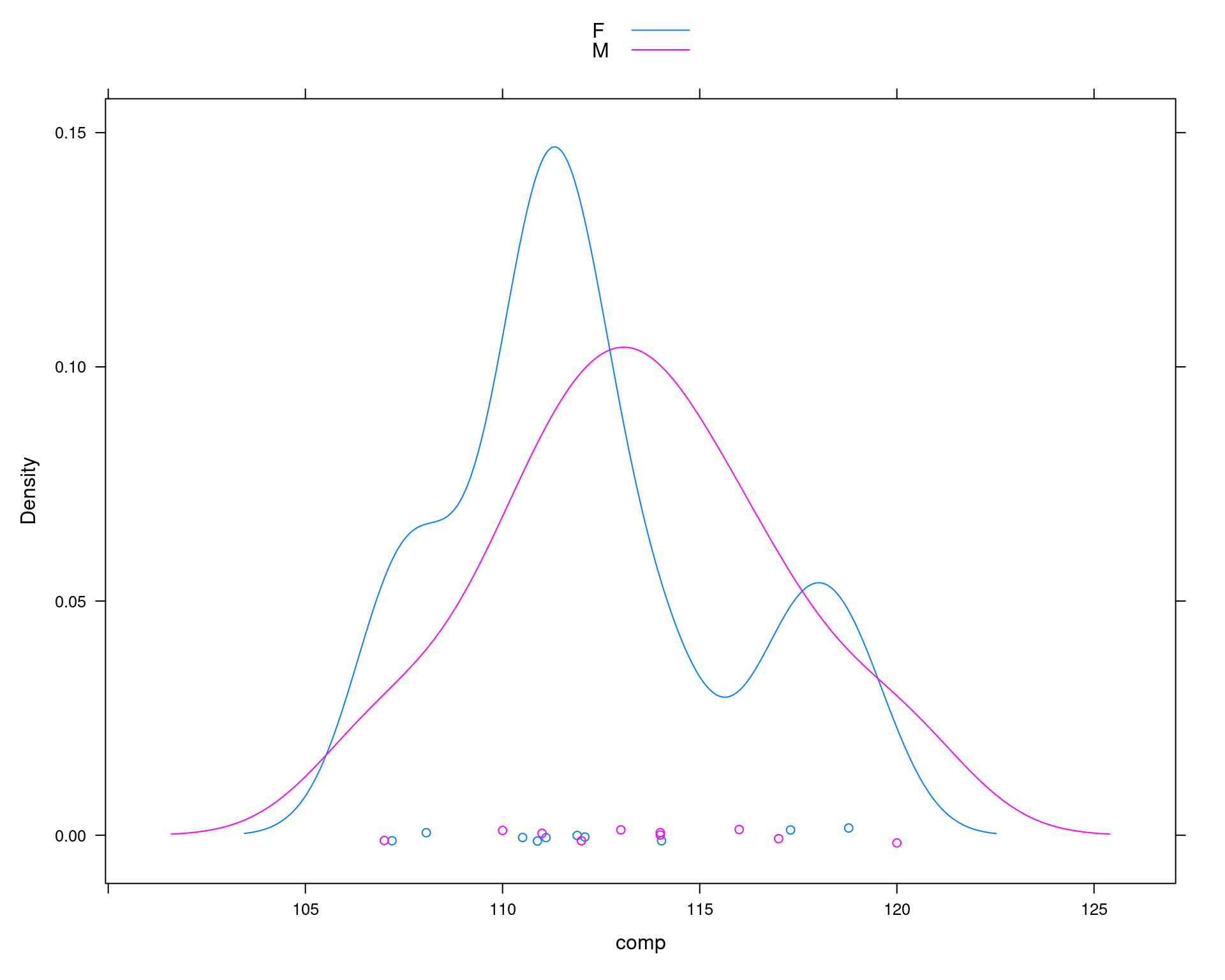

## Média por sexo
with(da, tapply(comp, sexo, mean))

#       F       M 
# 112.185 113.400

## Diferença das médias
with(da, diff(tapply(comp, sexo, mean)))

#        M 
# 1.214975

## Média de cada sexo
(m1 <- mean(machos))

# [1] 113.4

(m2 <- mean(femeas))

# [1] 112.185

## Diferença entre as médias amostrais
(med.amostral <- m1 - m2)

# [1] 1.214975

## Calcula o desvio padrão ponderado
n1 <- length(machos)
v1 <- var(machos)
n2 <- length(femeas)
v2 <- var(femeas)
(s.pond <- sqrt(((n1 - 1) * v1 + (n2 - 1) * v2)/(n1 + n2 - 2)))

# [1] 3.690024

## Teste de hipótese para
## H0: mu1 = mu2
## Ha: mu1 > mu2
mu0 <- 0
t.test(x = machos, y = femeas, alternative = "greater",
       var.equal = TRUE, mu = mu0)

# 
#   Two Sample t-test
# 
# data:  machos and femeas
# t = 0.73625, df = 18, p-value = 0.2355
# alternative hypothesis: true difference in means is greater than 0
# 95 percent confidence interval:
#  -1.646627       Inf
# sample estimates:
# mean of x mean of y 
#   113.400   112.185

## Estatística de teste
(tcalc <- (m1 - m2)/(s.pond * sqrt(1/n1 + 1/n2)))

# [1] 0.7362465

## Valor crítico
(tcrit <- qt(.025, df = n1 + n2 - 2, lower.tail = FALSE))

# [1] 2.100922

## p-valor
pt(tcalc, df = n1 + n2 - 2, lower.tail = FALSE)

# [1] 0.2355338

Teste por simulação via Bootstrap

Se a hipótese nula é verdadeira, então o comprimento das mandíbulas de machos e fêmeas são provenientes da mesma população, e portanto podem ser pensados como uma única amostra.

No Bootstrap fazemos então uma reamostragem COM REPOSIÇÃO dos 20 valores, e atribui aleatoriamente 10 para cada grupo (macho ou fêmea). Se forem de fato da mesma população, então as diferenças entre as médias devem ser próximas de zero.

## Amostra bootstrap
N <- 1e4
## Suposicao de igualdade
amostra <- c(machos, femeas)
## Bootstrap
am <- replicate(
    N, diff(tapply(sample(amostra, replace = TRUE), da$sexo, mean))
)
## Visualização
hist(am, main = "Distribuição amostral")
abline(v = med.amostral, col = 2)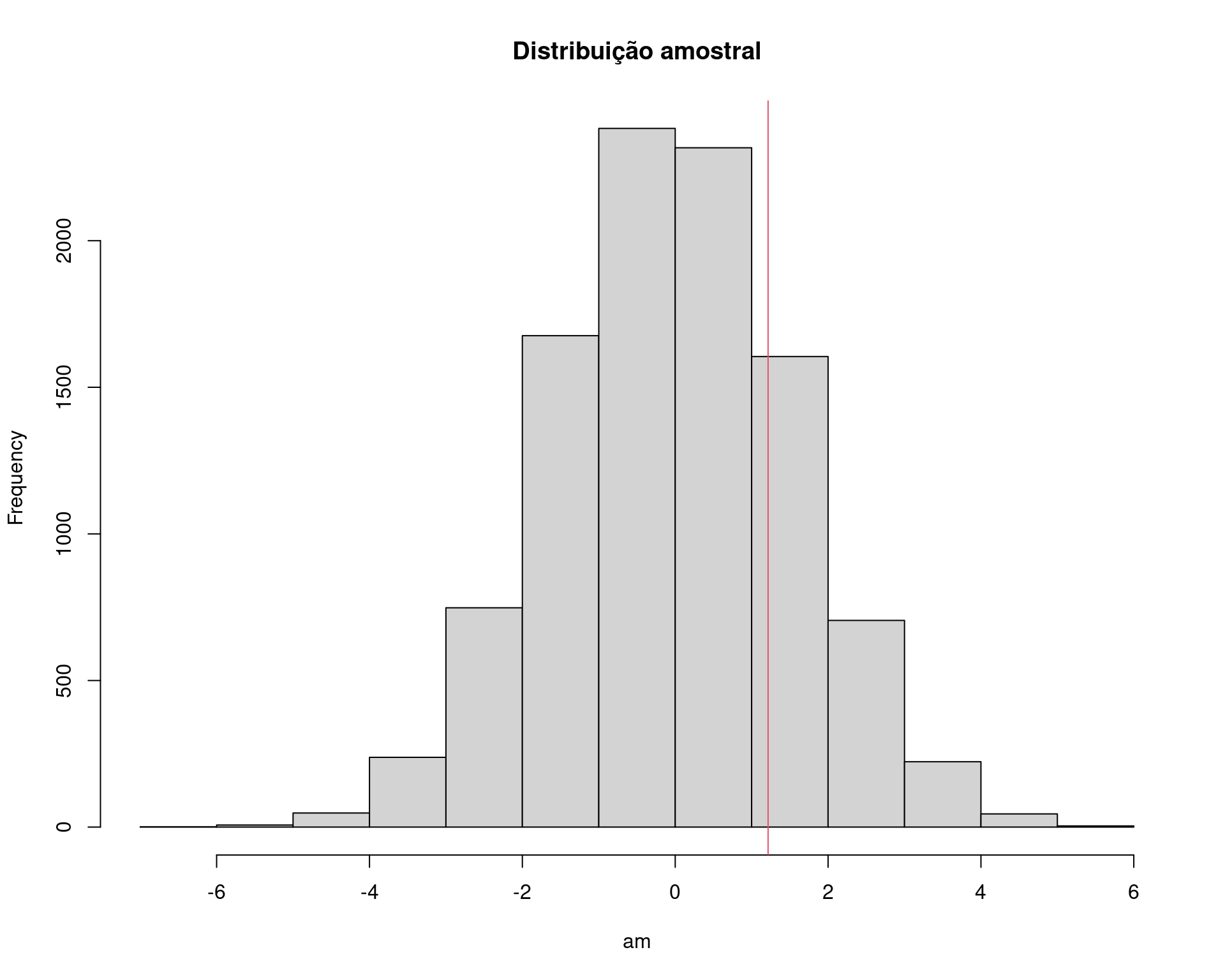

## p-valor empírico
sum(am >= med.amostral)/N

# [1] 0.2174

Exemplo original de Manly (1997)

## Comparação do comprimento da mandíbula de chacais machos e fêmeas
machos <- c(120, 107, 110, 116, 114, 111, 113, 117, 114, 112)
femeas <- c(110, 111, 107, 108, 110, 105, 107, 106, 111, 111)
da <- data.frame(comp = c(machos, femeas),
                 sexo = c(rep("M", 10), rep("F", 10)))
lattice::densityplot(~comp, groups = sexo, data = da, auto.key = TRUE)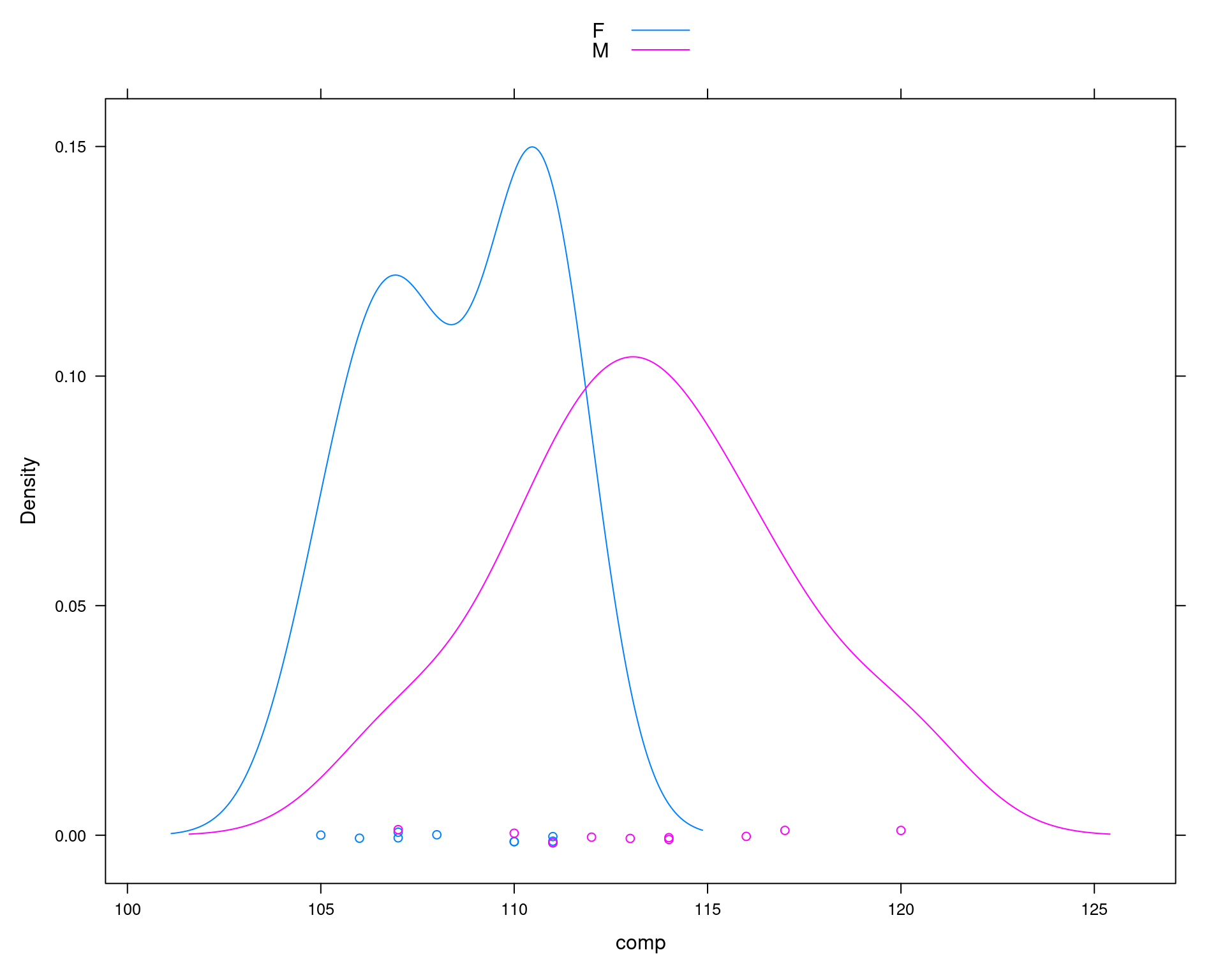

## Média por sexo
tapply(da$comp, da$sexo, mean)

#     F     M 
# 108.6 113.4

## Diferença das médias
diff(tapply(da$comp, da$sexo, mean))

#   M 
# 4.8

## Média de cada sexo
(m1 <- mean(machos))

# [1] 113.4

(m2 <- mean(femeas))

# [1] 108.6

## Diferença entre as médias amostrais
(med.amostral <- m1 - m2)

# [1] 4.8

## Calcula o desvio padrão ponderado
n1 <- length(machos)
v1 <- var(machos)
n2 <- length(femeas)
v2 <- var(femeas)
(s.pond <- sqrt(((n1 - 1) * v1 + (n2 - 1) * v2)/(n1 + n2 - 2)))

# [1] 3.080404

## Teste de hipótese para
## H0: mu1 = mu2
## Ha: mu1 > mu2
mu0 <- 0
t.test(x = machos, y = femeas, alternative = "greater",
       var.equal = TRUE, mu = mu0)

# 
#   Two Sample t-test
# 
# data:  machos and femeas
# t = 3.4843, df = 18, p-value = 0.001324
# alternative hypothesis: true difference in means is greater than 0
# 95 percent confidence interval:
#  2.411156      Inf
# sample estimates:
# mean of x mean of y 
#     113.4     108.6

## Estatística de teste
(tcalc <- (m1 - m2)/(s.pond * sqrt(1/n1 + 1/n2)))

# [1] 3.484324

## Valor crítico
(tcrit <- qt(.025, df = n1 + n2 - 2, lower.tail = FALSE))

# [1] 2.100922

## p-valor
pt(tcalc, df = n1 + n2 - 2, lower.tail = FALSE)

# [1] 0.001323634

## Teste por simulação via Bootstrap
N <- 1e5 # NOTE o aumento no número de simulações
## Simula direto da distribuição amostral
library(future.apply) # para um replicate mais eficiente (em paralelo)
plan(multicore, workers = 4)
## Suposicao de igualdade
amostra <- c(machos, femeas)
## Bootstrap
am <- future_replicate(
    N, diff(tapply(sample(amostra, replace = TRUE), da$sexo, mean))
)
## Visualização
hist(am, main = "Distribuição amostral")
abline(v = med.amostral, col = 2)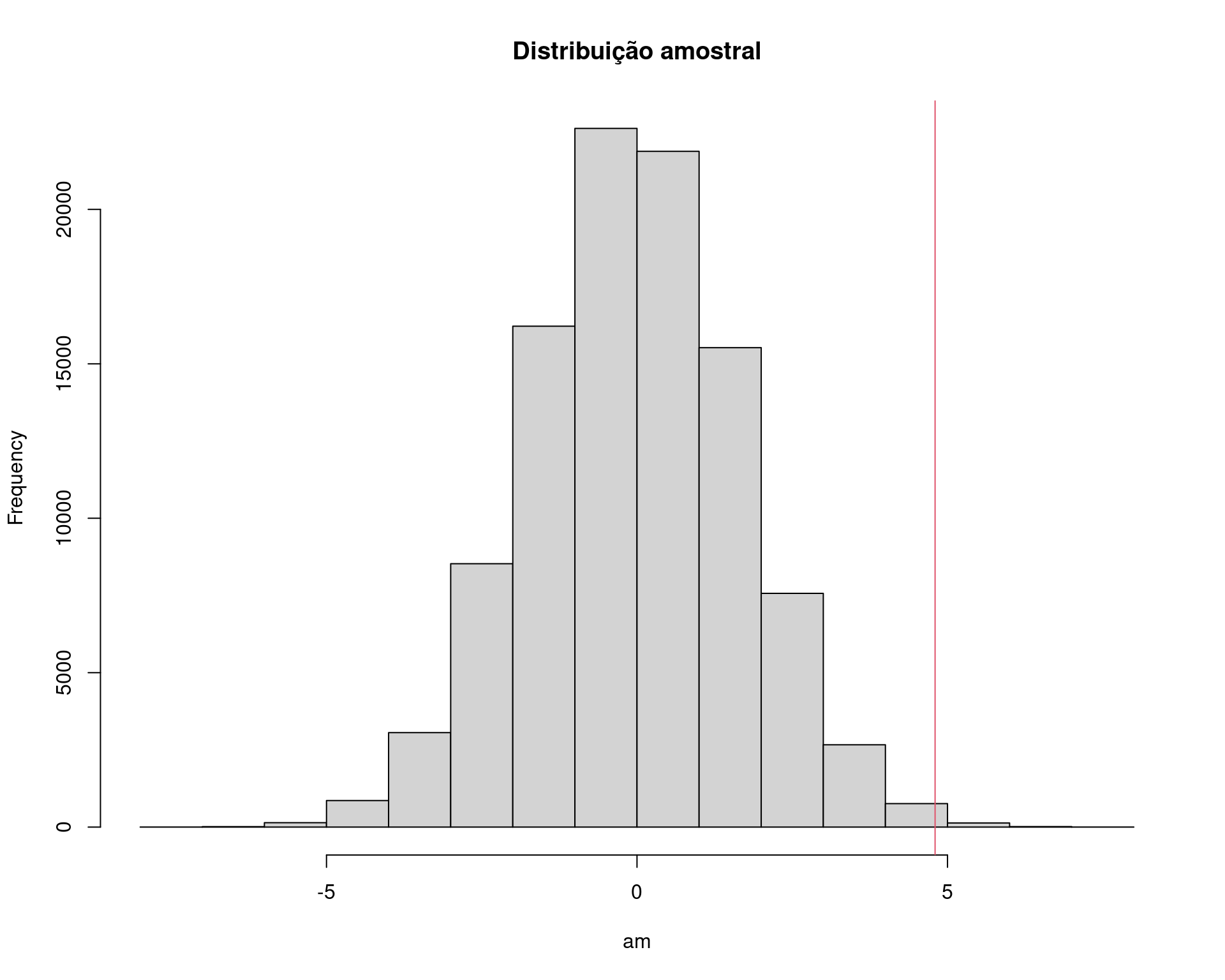

## p-valor empírico
sum(am >= med.amostral)/N

# [1] 0.00228

Uma nota de precaução

## Amostra de uma Poisson(2)
x <- c(2, 2, 1, 1, 5, 4, 4, 3, 1, 2)
## Distribuição empírica
prop.table(table(x))

# x
#   1   2   3   4   5 
# 0.3 0.3 0.1 0.2 0.1

## Distribuição empírica acumulada
cumsum(prop.table(table(x)))

#   1   2   3   4   5 
# 0.3 0.6 0.7 0.9 1.0

## Amostra via bootstrap
## Um passo
am <- sample(x, replace = TRUE)
prop.table(table(am))

# am
#   1   2   4   5 
# 0.1 0.5 0.3 0.1

cumsum(prop.table(table(am)))

#   1   2   4   5 
# 0.1 0.6 0.9 1.0

## B passos
B <- 1e4
am <- sample(x, size = B, replace = TRUE)
prop.table(table(am))

# am
#      1      2      3      4      5 
# 0.2989 0.3035 0.0938 0.2096 0.0942

cumsum(prop.table(table(am)))

#      1      2      3      4      5 
# 0.2989 0.6024 0.6962 0.9058 1.0000

## Qual o problema então?
## Distribuição empírica
plot(0:5, c(0, prop.table(table(am))), type = "h")
## Distribuição teórica
points((0:5) + .1, dpois(0:5, 2), type = "h", col = 2)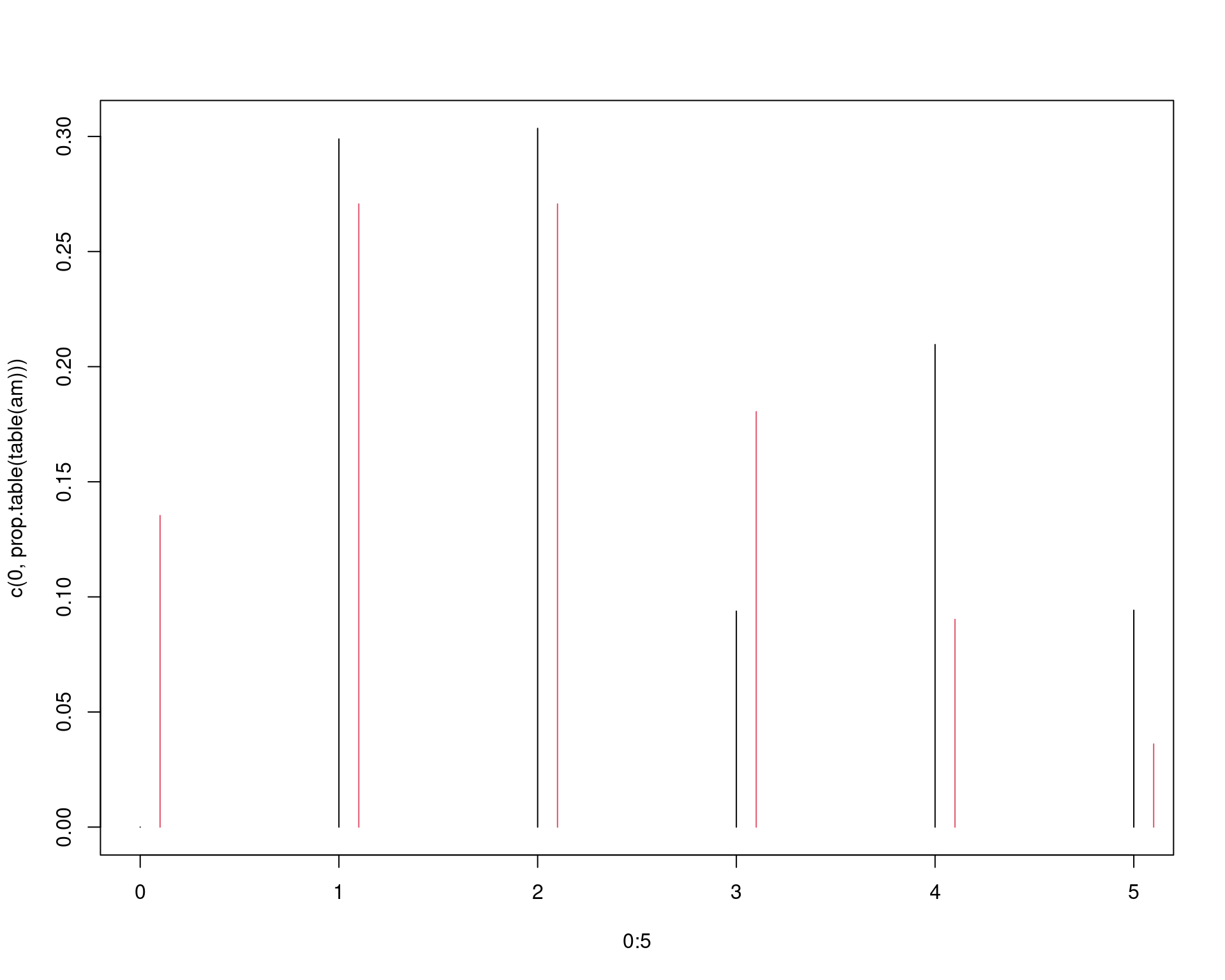

2 Estimativa de erro padrão via bootstrap

A estimativa do erro padrão de um estimador \(\hat{\theta}\) via bootstrap é o desvio padrão amostral das estimativas de bootstrap \(\hat{\theta}^{(1)}, \ldots, \hat{\theta}^{(B)}\)

\[ se(\hat{\theta}^{\star}) = \sqrt{\frac{1}{B-1} \sum_{b=1}^{B} (\hat{\theta}^{(b)} - \overline{\hat{\theta}^{\star}})} \]

2.1 Exemplo (notas)

## Estimativa de erro padrão via bootstrap
library(bootstrap) # para carregar os dados
## Uma amostra dos dados originais
str(law)

# 'data.frame': 15 obs. of  2 variables:
#  $ LSAT: num  576 635 558 578 666 580 555 661 651 605 ...
#  $ GPA : num  3.39 3.3 2.81 3.03 3.44 3.07 3 3.43 3.36 3.13 ...

with(law, plot(LSAT, GPA))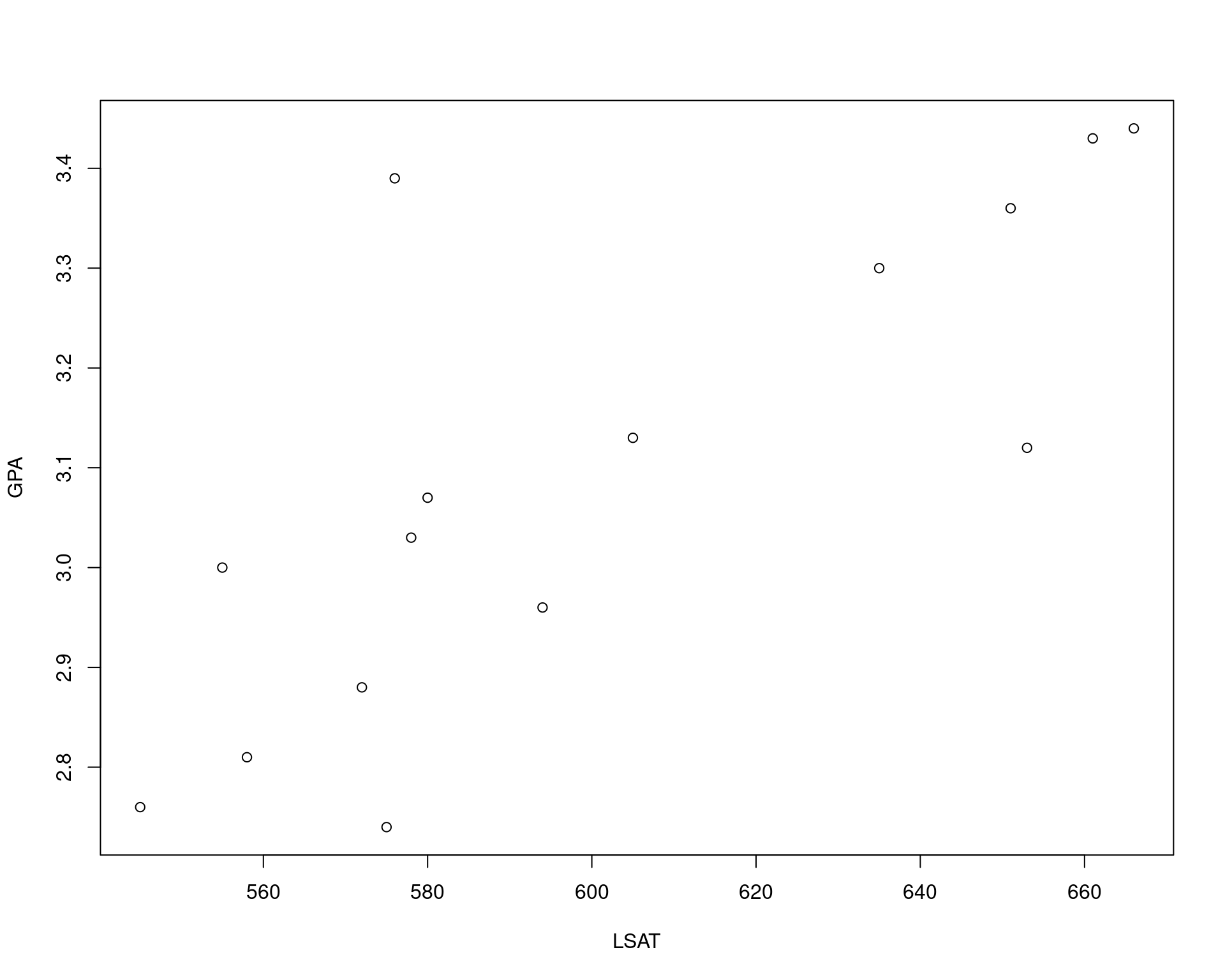

(coram <- with(law, cor(LSAT, GPA)))

# [1] 0.7763745

## Dados originais
str(law82)

# 'data.frame': 82 obs. of  3 variables:
#  $ School: num  1 2 3 4 5 6 7 8 9 10 ...
#  $ LSAT  : num  622 542 579 653 606 576 620 615 553 607 ...
#  $ GPA   : num  3.23 2.83 3.24 3.12 3.09 3.39 3.1 3.4 2.97 2.91 ...

with(law82, plot(LSAT, GPA))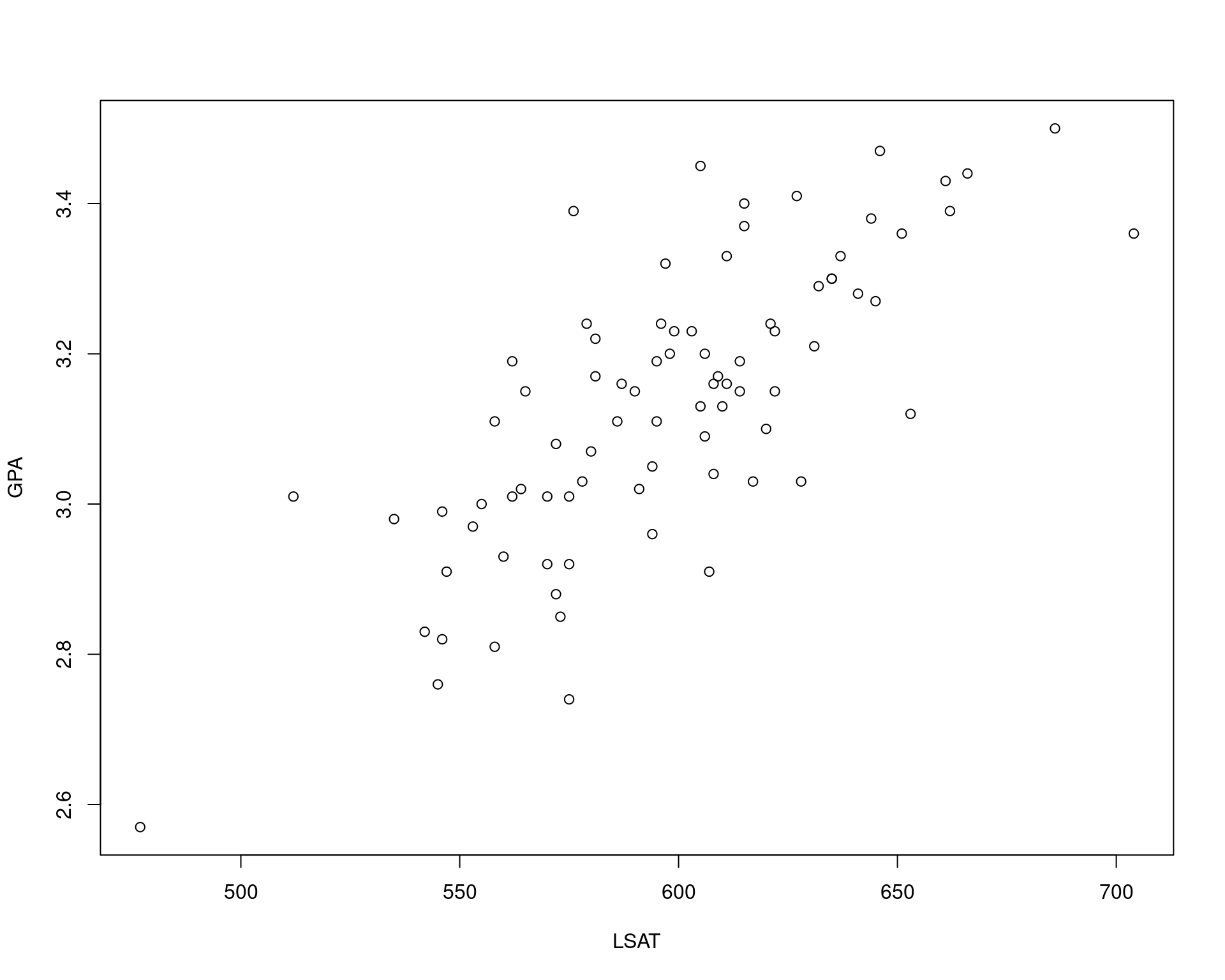

with(law82, cor(LSAT, GPA))

# [1] 0.7599979

## Definições
B <- 2000
n <- nrow(law)
R <- numeric(B)

## Bootstrap para a estimativa do erro padrão do R (correlação amostral)
for (b in 1:B) {
    i <- sample(1:n, size = n, replace = TRUE)
    LSAT <- law$LSAT[i]
    GPA <- law$GPA[i]
    R[b] <- cor(LSAT, GPA)
}

## Resultado
mean(R)

# [1] 0.7709778

(se.R <- sd(R))

# [1] 0.1368193

hist(R)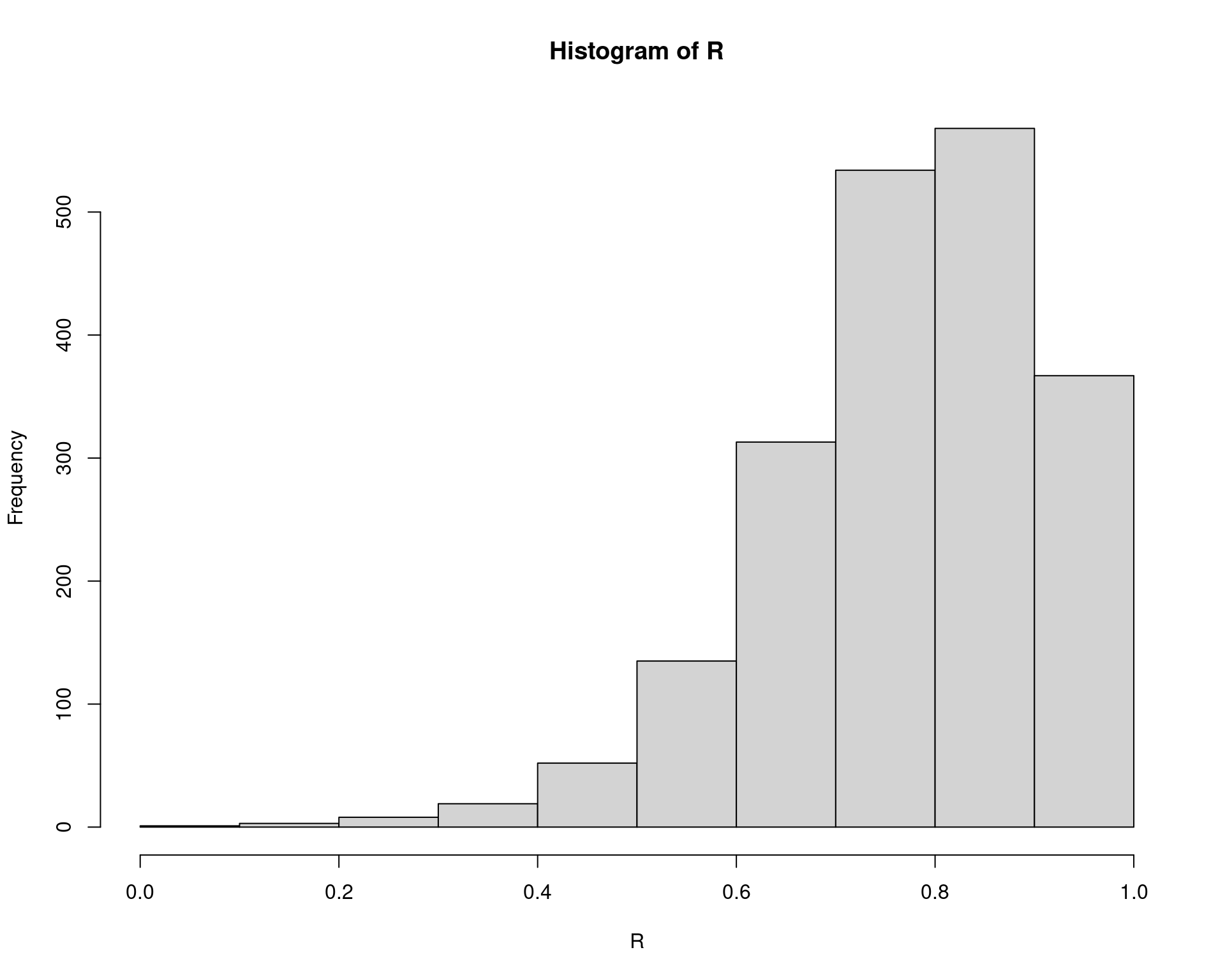

## sqrt((1 - coram^2)/(n - 2))
## (sd(law$GPA) * sqrt((1 - coram^2)))/(n - 2)

2.2 Exemplo (notas com boot)

Usando a função boot::boot() (Canty and Ripley 2022) que se baseia em Davison and Hinkley (1997).

## Define a função que calcula a estatística de interesse
r <- function(x, i) {
    cor(x[i, 1], x[i, 2])
}

## Roda o processo
library(boot)

# 
# Attaching package: 'boot'

# The following object is masked from 'package:lattice':
# 
#     melanoma

obj <- boot(data = law, statistic = r, R = 2000)
obj

# 
# ORDINARY NONPARAMETRIC BOOTSTRAP
# 
# 
# Call:
# boot(data = law, statistic = r, R = 2000)
# 
# 
# Bootstrap Statistics :
#      original       bias    std. error
# t1* 0.7763745 -0.001896919   0.1359209

str(obj)

# List of 11
#  $ t0       : num 0.776
#  $ t        : num [1:2000, 1] 0.848 0.801 0.763 0.855 0.75 ...
#  $ R        : num 2000
#  $ data     :'data.frame':    15 obs. of  2 variables:
#   ..$ LSAT: num [1:15] 576 635 558 578 666 580 555 661 651 605 ...
#   ..$ GPA : num [1:15] 3.39 3.3 2.81 3.03 3.44 3.07 3 3.43 3.36 3.13 ...
#  $ seed     : int [1:626] 10403 67 374337935 -66916328 796352990 -1344538218 7326455 801261936 -841320945 1823181309 ...
#  $ statistic:function (x, i)  
#   ..- attr(*, "srcref")= 'srcref' int [1:8] 2 6 4 1 6 1 2 4
#   .. ..- attr(*, "srcfile")=Classes 'srcfilecopy', 'srcfile' <environment: 0x55c397f3a2c8> 
#  $ sim      : chr "ordinary"
#  $ call     : language boot(data = law, statistic = r, R = 2000)
#  $ stype    : chr "i"
#  $ strata   : num [1:15] 1 1 1 1 1 1 1 1 1 1 ...
#  $ weights  : num [1:15] 0.0667 0.0667 0.0667 0.0667 0.0667 ...
#  - attr(*, "class")= chr "boot"
#  - attr(*, "boot_type")= chr "boot"

plot(obj)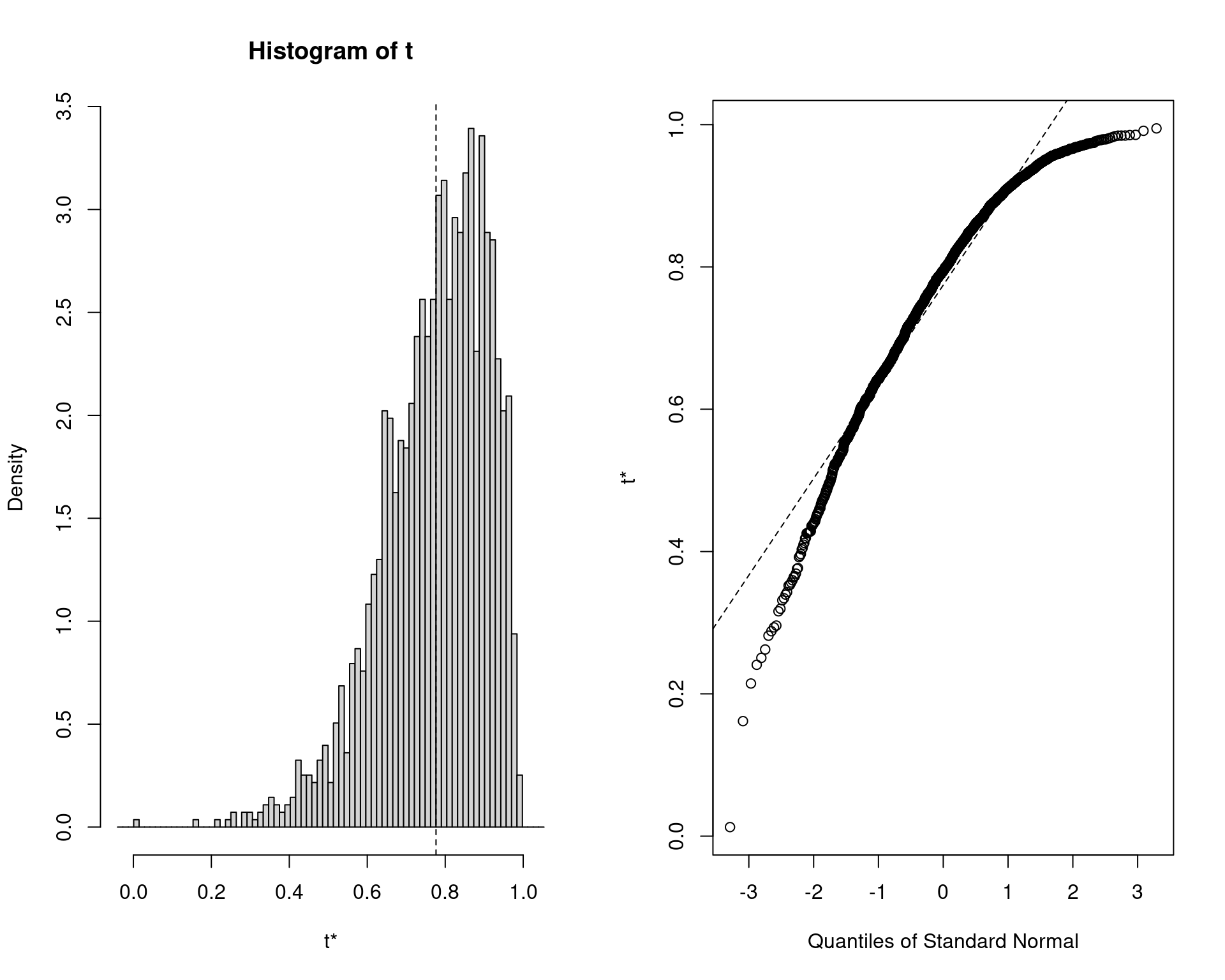

## Acessa os valores calculados
y <- as.vector(obj$t)
mean(y)

# [1] 0.7744776

sd(y)

# [1] 0.1359209

2.3 Exemplo (notas com bootstrap)

Usando a função bootstrap::bootstrap() (original, StatLib, and Rob Tibshirani. R port by Friedrich Leisch. 2019) que se baseia em Efron and Tibshirani (1993).

## Define a função que calcula a estatística
r <- function(x, xdata) {
    cor(xdata[x, 1], xdata[x, 2])
}

## Procedimento
n <- nrow(law)
obj2 <- bootstrap(x = 1:n, nboot = 2000, theta = r, law)
str(obj2)

# List of 5
#  $ thetastar     : num [1:2000] 0.689 0.545 0.775 0.719 0.614 ...
#  $ func.thetastar: NULL
#  $ jack.boot.val : NULL
#  $ jack.boot.se  : NULL
#  $ call          : language bootstrap(x = 1:n, nboot = 2000, theta = r, law)

mean(obj2$thetastar)

# [1] 0.7691919

sd(obj2$thetastar)

# [1] 0.1344538

3 Estimativa do viés via bootstrap

Se \(\hat{\theta}\) é um estimador não viesado para \(\theta\), então \(\text{E}[\hat{\theta}] = \theta\). O viés de um estimador \(\hat{\theta}\) de \(\theta\) é

\[ \text{B}[\hat{\theta}] = \text{E}[\hat{\theta} - \theta] = \text{E}[\hat{\theta}] - \theta \]

• A estimativa de viés via bootstrap usa as estimativas de bootstrap de \(\hat{\theta}\) para construir a distribuição amostral de \(\hat{\theta}\).

• Para a população finita \(x = (x_1, \ldots, x_n)\), o parâmetro é \(\hat{\theta}(x)\), e existem \(B\) estimativas \(\hat{\theta}^{(b)}\) independentes e identicamente distribuídas.

• A média amostral de \(\{\hat{\theta}^{(b)}\}\) é não viesada para o valor esperado \(\text{E}[\hat{\theta}^{\star}]\), então a estimativa de viés via bootsrap é \[ \widehat{\text{B}}[\hat{\theta}] = \overline{\hat{\theta}^{\star}} - \hat{\theta} \] onde \(\hat{\theta} = \hat{\theta}(x)\) é a estimativa calculada da amostra original.

• Valores positivos de viés indicam que, em média, tende a sobrestimar \(\theta\).

Correção de viés
Se um estimador é viesado gostaríamos de “corrigir” este estimador fazendo \[ \theta - \text{B}[\hat{\theta}],\] que tem valor esperado \[ \text{E}[\theta - \text{B}[\hat{\theta}]] = \text{E}[\hat{\theta}] - (\text{E}[\hat{\theta}] - \theta) = \theta\] e portanto não viesado. Entretanto esta quantidade depende do parâmetro e não pode ser calculada pela amostra. Utilizando a estimativa bootstrap do viés tem-se que: \[ \theta - \widehat{\text{B}}[\hat{\theta}].\] Desta forma uma estimativa \(\hat{\theta}^c\) para \(\theta\) corrigida pelo viés é: \[\begin{align} \hat{\theta}^c &= \hat{\theta} - \widehat{\text{B}}[\hat{\theta}] \\ &= \hat{\theta} - (\overline{\hat{\theta}^{\star}} - \hat{\theta}) \\ &= 2\hat{\theta} - \overline{\hat{\theta}^{\star}}, \end{align}\] ou seja, a estimativa corrigida é dada pelo dobro da original subtraída da médas das estimativas das amostras bootstrap.

## Estimativa do viés via bootstrap

## Estatística amostral
(theta.hat <- with(law, cor(LSAT, GPA)))

# [1] 0.7763745

## Definições
B <- 2000
n <- nrow(law)
theta.b <- numeric(B)

for (b in 1:B) {
    i <- sample(1:n, size = n, replace = TRUE)
    LSAT <- law$LSAT[i]
    GPA <- law$GPA[i]
    theta.b[b] <- cor(LSAT, GPA)
}

## Viés
mean(theta.b) - theta.hat

# [1] -0.0004970639

## Estimativa corrigida pelo viés
2 * theta.hat - mean(theta.b)

# [1] 0.7768716

4 Intervalos de confiança via Bootstrap

Existem diversas abordagens para o cálculo de intervalos de confiança via bootstrap. Os principais serão descritos abaixo.

4.1 Intervalo normal padrão

• É o método mais simples.
• Suponha que conhecemos \(\hat{\theta}\) e seu erro padrão \(se(\hat{\theta})\)
• Se \(\hat{\theta}\) é uma média, e o tamanho da amostra é grande, então o Teorema do Limite Central implica que \[ Z = \frac{\hat{\theta} - \text{E}[\hat{\theta}]}{se(\hat{\theta})} \] possui distribuição aproximadamente normal padrão.
• Portanto, se \(\hat{\theta}\) é um estimador não viesado para \(\theta\), então um intervalo \(100(1-\alpha)\%\) para \(\theta\) é \[ \hat{\theta} \pm z_{\alpha/2} se(\hat{\theta}) \]
• Esse intervalo é fácil de calcular, mas fizemos diversas suposições:
  • A distribuição de \(\hat{\theta}\) é normal
    • OU \(\hat{\theta}\) é uma média e o tamanho da amostra é grande
  • Também assumimos que \(\hat{\theta}\) é não viesado para \(\theta\)
  • Assumimos que \(se(\hat{\theta})\) é um parâmetro conhecido, mas no bootstrap \(se(\hat{\theta})\) é estimado (é o desvio padrão das amostras de bootstrap)

4.2 Intervalo básico de boostrap

• O intervalo básico de bootstrap transforma a distribuição das estimativas de boostrap, através da subtração da estatística observada
• Os quantis da amostra transformada \(\hat{\theta}^{\star} - \hat{\theta}\) são utilizados para a determinação dos limites de confiança
• O intervalo básico de bootstrap \(100(1-\alpha)\%\) de confiança é \[ ( 2\hat{\theta} - \hat{\theta}^{\star}_{1-\alpha/2}, \quad 2\hat{\theta} - \hat{\theta}^{\star}_{\alpha/2} ) \] onde \(\hat{\theta}^{\star}_{\alpha}\) denota o \(\alpha\)-quantil das estimativas de bootstrap \(\hat{\theta}^{\star}\). A derivação é longa e pode ser vista em Davison e Hinkley (1997).

4.3 Intervalo percentil de bootstrap

• O intervalo percentil de bootstrap usa a distribuição empírica das estimativas de bootstrap como distribuição de referência
• Os quantis da distribuição empírica são estimadores dos quantis da distribuição amostral de \(\hat{\theta}\)
  • Estas quantidades (aleatórias) devem devem ser mais próximas das verdadeiras quando esta distribuição amostral é normal
• Suponha que \(\hat{\theta}^{(1)}, \ldots, \hat{\theta}^{B}\) são as estimativas de bootstrap de \(\hat{\theta}\)
• A partir da distribuição empírica das estimativas, determine os quantis \(\alpha/2\) e \(1-\alpha/2\) de \(\hat{\theta}\)
• Portanto o intervalo percentil de bootstrap \(100(1-\alpha)\%\) é \[ (\hat{\theta}_{\alpha/2}^{\star}, \hat{\theta}_{1-\alpha/2}^{\star}) \]
• Pode-se mostrar que o intervalo percentil de bootstrap possui vantagens teóricas e maior taxa de cobertura, quando comparado aos intervalos normal e básico

A função boot::boot.ci() calcula estes três tipos de intervalos

## Exemplo para correlação

## Define a função que calcula a estatística de interesse
r <- function(x, i) {
    cor(x[i, 1], x[i, 2])
}

## Roda o processo
boot.obj <- boot(data = law, statistic = r, R = 2000)
## Resumo
boot.obj

# 
# ORDINARY NONPARAMETRIC BOOTSTRAP
# 
# 
# Call:
# boot(data = law, statistic = r, R = 2000)
# 
# 
# Bootstrap Statistics :
#      original       bias    std. error
# t1* 0.7763745 -0.008545694   0.1334486

## Estatística amostral
boot.obj$t0

# [1] 0.7763745

## Viés
(vies <- mean(boot.obj$t) - boot.obj$t0)

# [1] -0.008545694

## Distribuição das estimativas de bootstrap
plot(boot.obj)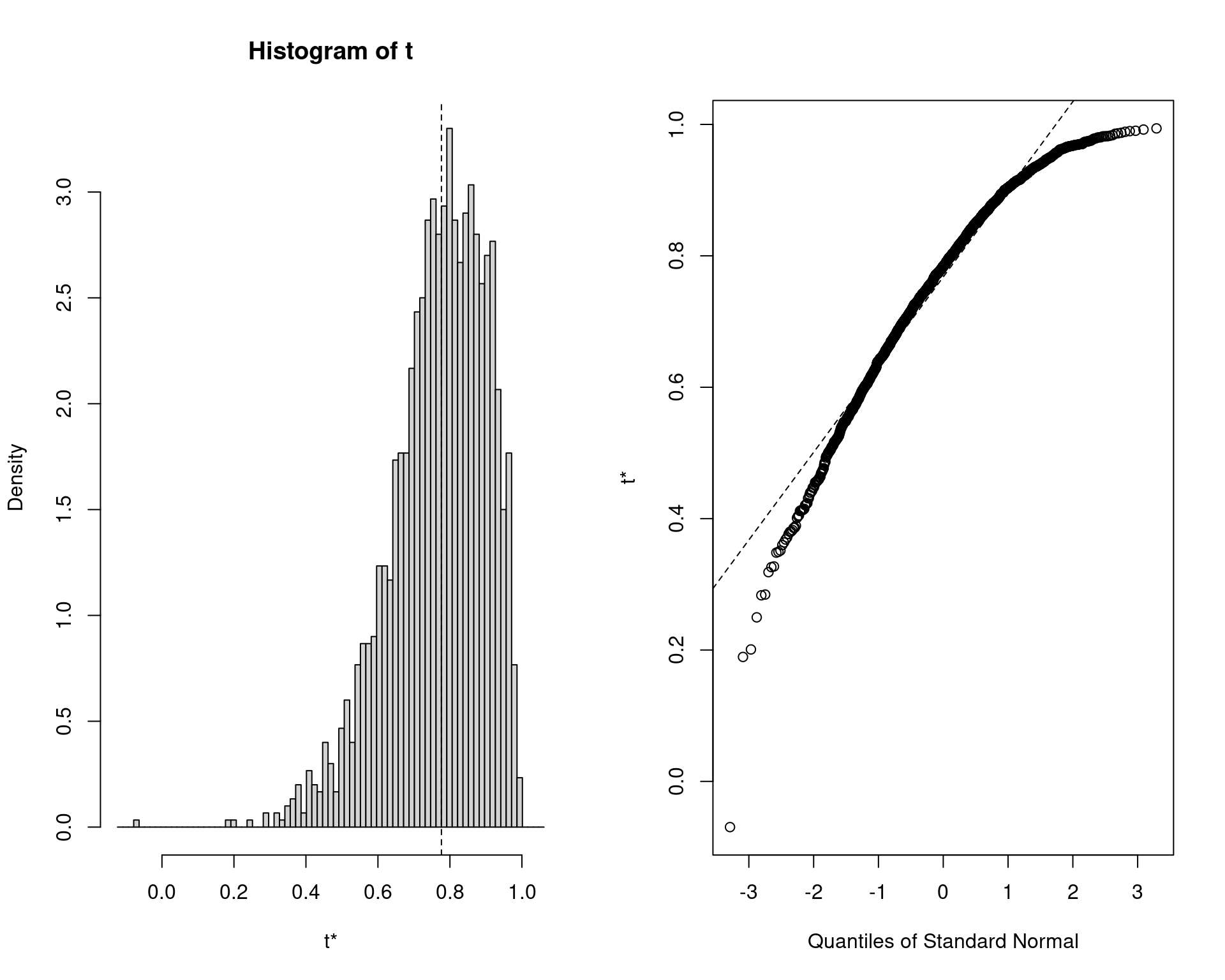

## Intervalos
boot.ci(boot.obj, type = c("basic", "norm", "perc"))

# BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
# Based on 2000 bootstrap replicates
# 
# CALL : 
# boot.ci(boot.out = boot.obj, type = c("basic", "norm", "perc"))
# 
# Intervals : 
# Level      Normal              Basic              Percentile     
# 95%   ( 0.5234,  1.0465 )   ( 0.5859,  1.0971 )   ( 0.4557,  0.9669 )  
# Calculations and Intervals on Original Scale

Calcula intervalos manualmente

## Define intervalo com alpha = 0.05
alpha <- c(.025, .975)

## Normal
(theta.hat <- boot.obj$t0)

# [1] 0.7763745

(se.theta <- sd(boot.obj$t))

# [1] 0.1334486

theta.hat + qnorm(alpha) * se.theta

# [1] 0.5148201 1.0379289

## Note que é diferente do resultado da função pois a função corrige
## pelo viés internamente
(theta.hat + qnorm(alpha) * se.theta) - vies

# [1] 0.5233658 1.0464746

boot.ci(boot.obj, type = "norm")

# BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
# Based on 2000 bootstrap replicates
# 
# CALL : 
# boot.ci(boot.out = boot.obj, type = "norm")
# 
# Intervals : 
# Level      Normal        
# 95%   ( 0.5234,  1.0465 )  
# Calculations and Intervals on Original Scale

## Básico
2 * theta.hat - quantile(boot.obj$t, probs = rev(alpha), type = 6)

#     97.5%      2.5% 
# 0.5858779 1.0970886

boot.ci(boot.obj, type = "basic")

# BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
# Based on 2000 bootstrap replicates
# 
# CALL : 
# boot.ci(boot.out = boot.obj, type = "basic")
# 
# Intervals : 
# Level      Basic         
# 95%   ( 0.5859,  1.0971 )  
# Calculations and Intervals on Original Scale

## Percentil
quantile(boot.obj$t, probs = alpha, type = 6)

#      2.5%     97.5% 
# 0.4556604 0.9668711

boot.ci(boot.obj, type = "perc")

# BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
# Based on 2000 bootstrap replicates
# 
# CALL : 
# boot.ci(boot.out = boot.obj, type = "perc")
# 
# Intervals : 
# Level     Percentile     
# 95%   ( 0.4557,  0.9669 )  
# Calculations and Intervals on Original Scale

Observações:

1. A função quantile() possui 9 formas diferentes de calcular os quantis, por isso aqui foi escolhido type = 6 para ficar mais próximo do que é usado internamente na função boot::boot.ci() (veja ?quantile)
2. O intervalo normal fornecido pela função é corrigido pelo viés (bias corrected ou intervalo BCa)
3. A grande diferença entre os limites dos intervalos normal e percentil é que a distribuição amostral da correlação não é normal (veja gráfico acima)
   • Quanto mais próxima a distribuição amostral de uma estatística for da normal, mais próximos serão o resultado destes dois intervalos
4. Note que o limite superior de alguns intervalos são maiores do que 1, o que para uma correlação não faz sentido.

4.4 Intervalo \(t\) de bootstrap

• No intervalo normal (acima), assumimos que \[ Z = \frac{\hat{\theta} - \text{E}[\hat{\theta}]}{se(\hat{\theta})} \sim \text{N}(0,1) \] Mas:
  • A distribuição normal para \(Z\) não é necessariamente correta, pois \(se(\hat{\theta})\) é estimado (e não conhecido)
  • Alternativamente poderiamos usar uma distribuição \(t\), mas a distribuição amostral de \(\widehat{se}(\hat{\theta})\) é desconhecida
• O intervalo \(t\) de bootstrap não usa uma distribuição \(t\) de Student como referência
• No entanto, uma distribuição “tipo \(t\)” (estudentizada) é gerada por reamostragem

Suponha que \(x = (x_1, \ldots, x_n)\) é uma amostra observada. O intervalo \(100(1-\alpha)\%\) \(t\) de bootstrap é \[ (\hat{\theta} - t^{\star}_{1-\alpha/2} \widehat{se}(\hat{\theta}), \quad \hat{\theta} - t^{\star}_{\alpha/2} \widehat{se}(\hat{\theta}) ) \] onde \(\widehat{se}(\hat{\theta})\), \(t^{\star}_{\alpha/2}\), e \(t^{\star}_{1-\alpha/2}\) são calculados conforme o algoritmo abaixo.

1. Calcule a estatística observada \(\hat{\theta}\).
2. Para cada amostra indexada \(b = 1, \ldots, B\):
   1. Amostre com reposição de \(x\) para gerar a \(b\)-ésima amostra \(x^{(b)} = (x_{1}^{(b)}, \ldots, x_{n}^{(b)})\)
   2. Calcule \(\hat{\theta}^{(b)}\) da \(b\)-ésima amostra \(x^{(b)}\)
   3. Calcule a estimativa de erro padrão \(\widehat{se}(\hat{\theta}^{(b)})\) (NOTE que essa é uma estimativa separada para cada amostra de bootstrap \(x^{(b)}\), e não \(x\))
   4. Calcule a \(b\)-ésima estimativa da estatística \(t\) \[ t^{(b)} = \frac{\hat{\theta}^{(b)} - \hat{\theta}}{\widehat{se}(\hat{\theta}^{(b)})} \]
3. A amostra de estimativas \(t^{(1)}, \ldots, t^{(B)}\) é a distribuição de referência para o intervalo \(t\). Encontre os quantis amostrais \(t^{\star}_{\alpha/2}\) e \(t^{\star}_{1-\alpha/2}\) da amostra ordenada \(t^{(b)}\)
4. Calcule \(\widehat{se}(\hat{\theta})\), ou seja, o desvio padrão amostral das estimativas \(\hat{\theta}^{(b)}\)
5. Calcule os limites de confiança \[ (\hat{\theta} - t^{\star}_{1-\alpha/2} \widehat{se}(\hat{\theta}), \quad \hat{\theta} - t^{\star}_{\alpha/2} \widehat{se}(\hat{\theta}) ) \]

• Uma desvantagem deste método é que as estimativas \(\widehat{se}(\hat{\theta}^{(b)})\) são também obtidas via bootstrap, ou seja, é um bootstrap dentro de outro bootstrap, o que torna o método muito mais caro computacionalmente.

## Define função geral para calcular o intervalo t de bootstrap
boot.t.ci <- function(x, B = 500, R = 100, level = .95, statistic){
    ## B = número de estimativas bootstrap (geral)
    ## R = número de estimativas bootstrap para o erro padrão
    x <- as.matrix(x);  n <- nrow(x)
    stat <- numeric(B); se <- numeric(B)
    ## Função local para calcular o erro padrão de cada amostra
    ## bootstrap x^{(b)} => bootstrap dentro de bootstrap
    boot.se <- function(x, R, f) {
        x <- as.matrix(x); m <- nrow(x)
        th <- replicate(R, expr = {
            i <- sample(1:m, size = m, replace = TRUE)
            ## f() é uma função = estatística calculada de interesse
            f(x[i, ])
        })
        return(sd(th))
    }
    ## Bootstrap geral
    for (b in 1:B) {
        j <- sample(1:n, size = n, replace = TRUE)
        y <- x[j, ]
        ## Calcula a estatística de interesse
        stat[b] <- statistic(y)
        ## Calcula o erro padrão baseado na amostra x^{(b)}. Aqui é
        ## feito um bootstrap dentro do outro
        se[b] <- boot.se(y, R = R, f = statistic)
    }
    ## Estatística amostral
    stat0 <- statistic(x)
    ## Estatística "estudentizada"
    t.stats <- (stat - stat0)/se
    ## Erro padrão das estimativas de bootstrap
    se0 <- sd(stat)
    ## Define alpha com base no nível de confiança
    alpha <- 1 - level
    ## Determina os quantis da distribuição da estatística
    ## "estudentizada"
    Qt <- quantile(t.stats, c(alpha/2, 1 - alpha/2), type = 1)
    ## Calcule limites do intervalo (inverte os nomes)
    CI <- rev(stat0 - Qt * se0)
    names(CI) <- rev(names(CI))
    return(list(CI = CI, stat = stat,
                t.stats = t.stats, Qt = Qt))
}

## Aplica a função
ci <- boot.t.ci(law, statistic = r, B = 2000, R = 200)

## Resultados
ci$CI

#       2.5%      97.5% 
# -0.2431553  0.9856186

ci$Qt

#      2.5%     97.5% 
# -1.565874  7.629633

length(ci$stat)

# [1] 2000

length(ci$t.stats)

# [1] 2000

## Distribuições
par(mfrow = c(1, 2))
## Distribuição amostral
hist(ci$stat, xlim = c(-0.5, 1)); abline(v = ci$CI, col = 2)
## Distribuição "estudentizada" de referência
hist(ci$t.stats); abline(v = ci$Qt, col = 2)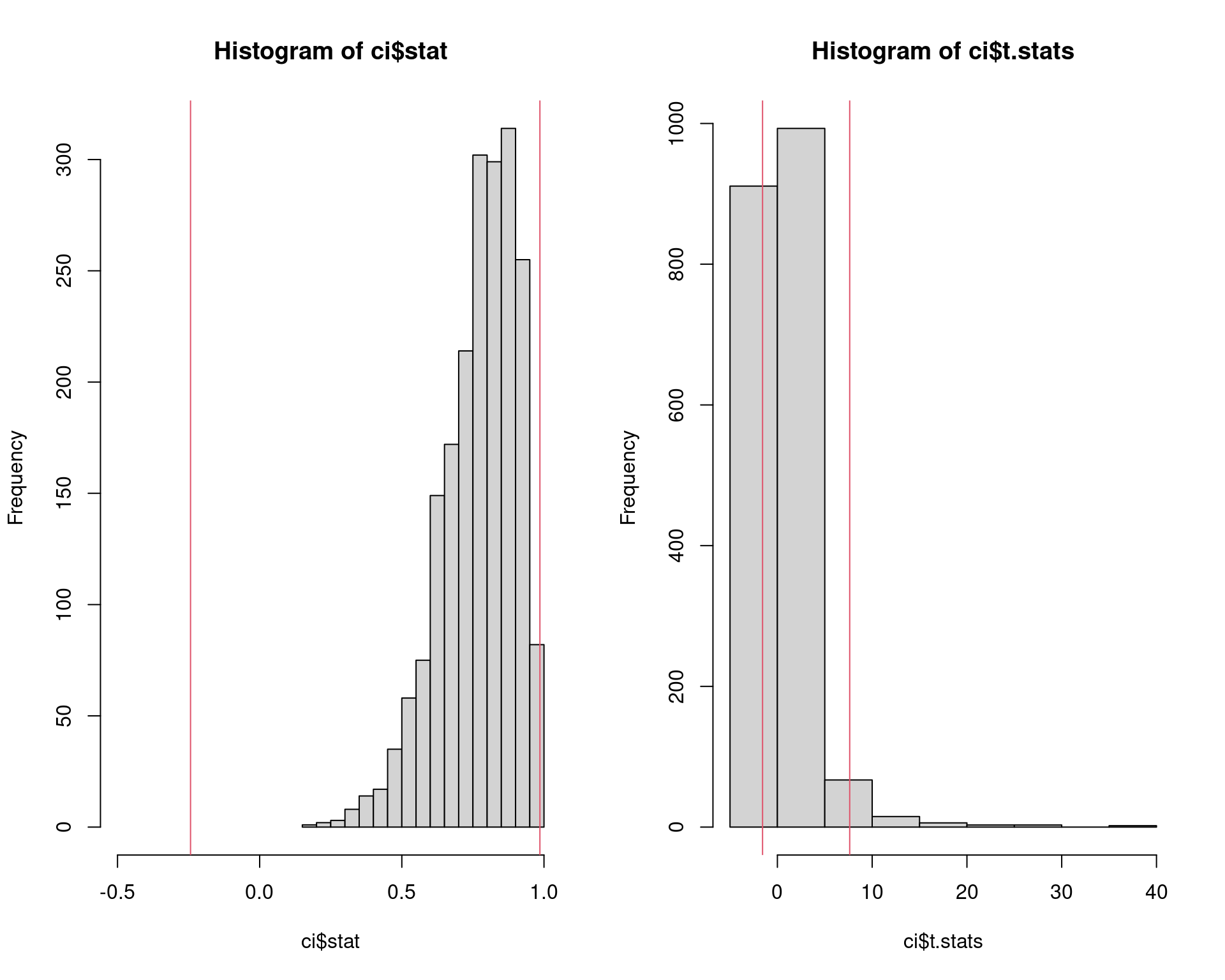

par(mfrow = c(1, 1))

Observações:

• Note que o limite inferior do intervalo é bem menor do que os demais
• O intervalo \(t\) de bootstrap é o que possui maior amplitude entre todos

Outro exemplo

A base de dados patch do pacote bootstrap contém dados de 8 pacientes que usaram adesivos (patches) contendo um certo hormônio que é injetado na corrente sanguínea. Cada indivíduo teve seu nível de hormônio medido após usar três diferentes adesivos: placebo, “antigo” (já utilizado), e “novo” (nova versão).

O objetivo do estudo é mostrar que existe bioequivalência, ou seja, que os adesivos novos são bioequivalentes aos antigos e podem ser liberados para uso.

O parâmetro de interesse é definida como \[ \theta = \frac{\text{E}[\text{novo}] - \text{E}[\text{velho}]} {\text{E}[\text{velho}] - \text{E}[\text{placebo}]} \]

Se \(|\theta| \leq 0.2\), então isso indica que existe bioequivalência entre os adesivos.

Os dados são

data(patch, package = "bootstrap")
patch

#   subject placebo oldpatch newpatch     z     y
# 1       1    9243    17649    16449  8406 -1200
# 2       2    9671    12013    14614  2342  2601
# 3       3   11792    19979    17274  8187 -2705
# 4       4   13357    21816    23798  8459  1982
# 5       5    9055    13850    12560  4795 -1290
# 6       6    6290     9806    10157  3516   351
# 7       7   12412    17208    16570  4796  -638
# 8       8   18806    29044    26325 10238 -2719

Onde:

• \(z = \text{velho} - \text{placebo}\)
• \(y = \text{novo} - \text{velho}\)

Portanto, a estatística de interesse é \[ \hat{\theta} = \frac{\bar{Y}}{\bar{Z}} \]

## Estimativas básicas
(theta.hat <- mean(patch$y)/mean(patch$z))

# [1] -0.0713061

## Bootstrap para erro padrão
n <- nrow(patch)
B <- 2000
theta.b <- numeric(B)
for (b in 1:B) {
    i <- sample(1:n, size = n, replace = TRUE)
    y <- patch$y[i]
    z <- patch$z[i]
    theta.b[b] <- mean(y)/mean(z)
}

## Estimativas
mean(theta.b)

# [1] -0.06287142

(bias <- mean(theta.b) - theta.hat)

# [1] 0.008434677

(se <- sd(theta.b))

# [1] 0.1011584

hist(theta.b)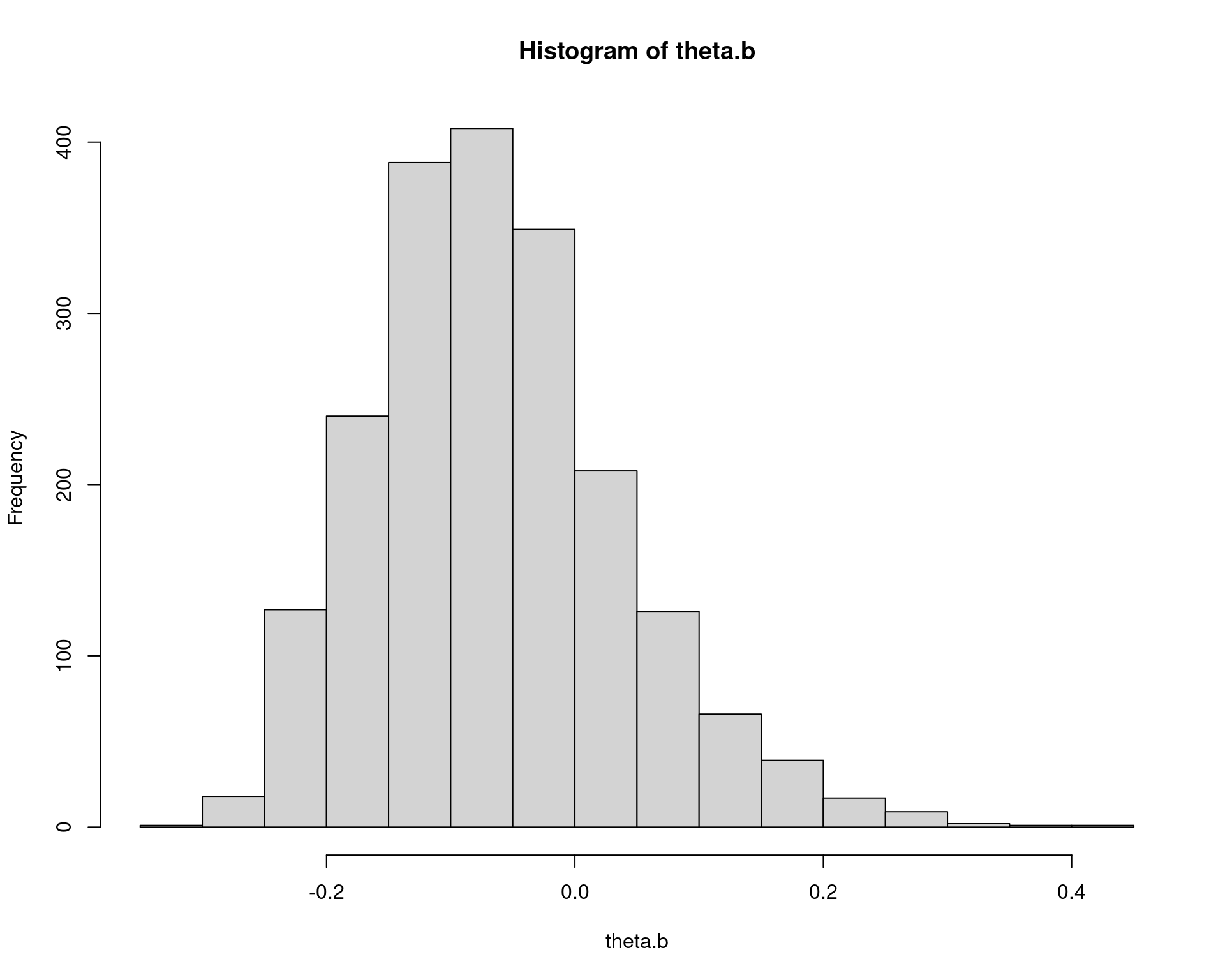

## Intervalos de confiança para a estimativa
## Usando o pacote boot
theta.boot <- function(dat, ind) {
    y <- dat[ind, 1]
    z <- dat[ind, 2]
    mean(y)/mean(z)
}

dat <- cbind(patch$y, patch$z)
boot.obj <- boot(dat, statistic = theta.boot, R = 2000)
boot.obj

# 
# ORDINARY NONPARAMETRIC BOOTSTRAP
# 
# 
# Call:
# boot(data = dat, statistic = theta.boot, R = 2000)
# 
# 
# Bootstrap Statistics :
#       original      bias    std. error
# t1* -0.0713061 0.008436566   0.1025824

hist(boot.obj$t)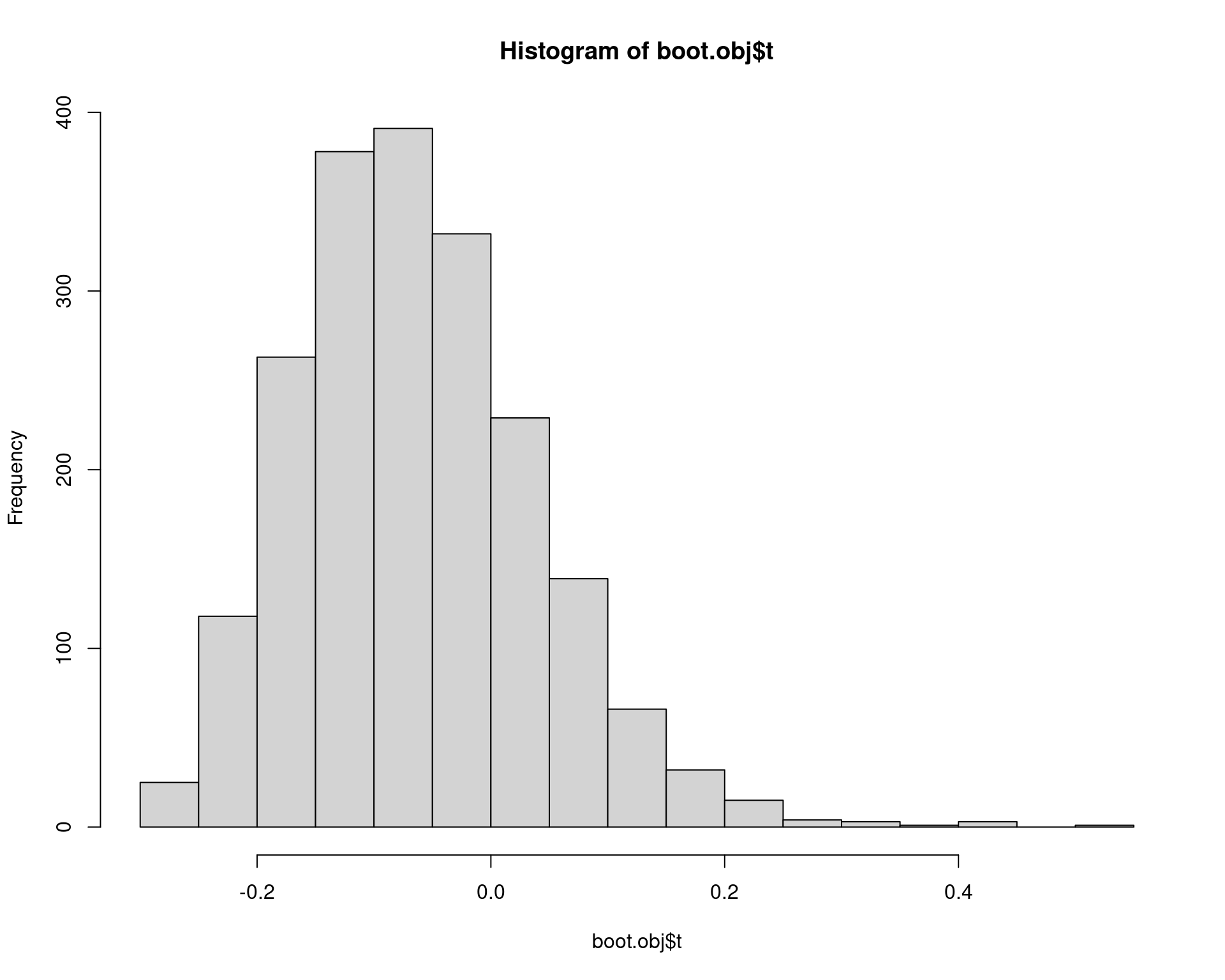

boot.ci(boot.obj, type = c("basic", "norm", "perc"))

# BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
# Based on 2000 bootstrap replicates
# 
# CALL : 
# boot.ci(boot.out = boot.obj, type = c("basic", "norm", "perc"))
# 
# Intervals : 
# Level      Normal              Basic              Percentile     
# 95%   (-0.2808,  0.1213 )   (-0.3045,  0.0914 )   (-0.2340,  0.1619 )  
# Calculations and Intervals on Original Scale

## Intervalo t de bootstrap
ci <- boot.t.ci(dat, statistic = theta.boot, B = 2000, R = 200)
ci$CI

#       2.5%      97.5% 
# -0.2653063  0.4066662

Lembre que se \(|\theta| \leq 0.2\) ou \(-0.2 \leq \theta \leq 0.2\), então os adesivos são bioequivalentes. Pelos intervalos, não é possível fazer essa afirmação.

5 Exercício

Simula de um modelo linear: \[ Y_i = \beta_0 + \beta_1 X_i + \epsilon_i, \quad i = 1, \ldots, n \] Onde: \[ \begin{aligned} X_i &\sim N(150, 15^2) \\ \epsilon_i &\sim N(0, \sigma^2) \\ \beta_0 &= 10 \\ \beta_1 &= 0.5 \\ \sigma^2 &= 20 \\ n &= 30 \end{aligned} \]

E, para todos os parâmetros (supostamente) desconhecidos (\(\beta_0\), \(\beta_1\) e \(\sigma^2\)):

1. Identifique as distribuições assintóticas dos estimadores de máxima verossimilhança e
   • Obtenha as estimativas pontuais
   • Obtenha os erros-padrão
   • Calcule intervalos de confiança
2. Faça uma simulação de bootstrap (não paramétrico) com \(B = 10000\) repetições para construir as distribuições amostrais empíricas e
   • Obtenha as estimativas pontuais
   • Obtenha os erros-padrão
   • Calcule intervalos de confiança (percentil e \(t\))
3. Repita o item acima com \(B = 100000\) repetições
4. Compare as distribuições amostrais, estimativas pontuais e erros-padrão obtidos nos itens acima.

Perguntas:

• As distribuições amostrais, estimativas pontuais e erros-padrão obtidos via bootstrap parecem estar de acordo com a teoria assintótiica?
• No bootstrap, o que acontece quando \(B\) aumenta?

Referências

Canty, Angelo, and B. D. Ripley. 2022. Boot: Bootstrap r (s-Plus) Functions.

Davison, A. C., and D. V. Hinkley. 1997. Bootstrap Methods and Their Applications. Cambridge: Cambridge University Press. http://statwww.epfl.ch/davison/BMA/.

Efron, Bradley, and Robert J. Tibshirani. 1993. An Introduction to the Bootstrap. Monographs on Statistics and Applied Probability 57. Boca Raton, Florida, USA: Chapman & Hall/CRC.

original, S, from StatLib, and by Rob Tibshirani. R port by Friedrich Leisch. 2019. Bootstrap: Functions for the Book "an Introduction to the Bootstrap". https://CRAN.R-project.org/package=bootstrap.

---

Este conteúdo está disponível por meio da Licença Creative Commons 4.0