2 Objetos e classes

2.1 Funções e argumentos

As funções no R são definidas como:

nome(argumento1, argumento2, ...)

Exemplo: função runif() (para gerar valores aleatórios de uma distribuição uniforme):

runif(n, min = 0, max = 1)

runif(10, 1, 100)
 [1] 31.468845 26.509578 55.679921  6.581932 47.386379 48.893303 81.427859
 [8] 37.661733 55.109301 17.855943

Argumentos que já possuem um valor especificado (como max e min) podem ser omitidos:

runif(10)

Se os argumentos forem nomeados, a ordem deles dentro da função não tem mais importância:

runif(min = 1, max = 100, n = 10)

Argumentos nomeados e não nomeados podem ser utilizados, desde que os não nomeados estejam na posição correta:

runif(10, max = 100, min = 1)

2.1.1 Outros tipos de argumentos

Exemplo: função sample():

sample(x, size, replace = FALSE, prob = NULL)

• x e size devem ser obrigatoriamente especificados.
• replace é lógico: TRUE (T) ou FALSE (F).
• prob é um argumento vazio ou ausente (“opcional”).

Exemplo: função plot():

plot(x, y, ...)

• “...” permite especificar argumentos de outras funções (por exemplo par()).

Para ver todos os argumentos disponíveis de uma função, podemos usar a função args().

args(sample)
function (x, size, replace = FALSE, prob = NULL) 
NULL

2.2 Mecanismos de ajuda

Argumentos e detalhes do funcionamento das funções:

?runif

ou

help(runif)

A documentação contém os campos:

• Description: breve descrição.
• Usage: função e todos seus argumentos.
• Arguments: lista descrevendo cada argumento.
• Details: descrição detalhada.
• Value: o que a função retorna.
• References: bibliografia relacionada.
• See Also: funções relacionadas.
• Examples: exemplos práticos.

Procura por nomes de funções que contenham algum termo:

apropos("mod")
apropos("model")

Procura por funções que contenham palavra em qualquer parte de sua documentação:

help.search("palavra")

Ajuda através do navegador (também contém manuais, …):

help.start()

Sites para busca na documentação dos diversos pacotes:

• RDocumentation https://www.rdocumentation.org/.
• R Package Documentation https://rdrr.io/.
• R Contributed Documentation (várias línguas). https://cran.r-project.org/other-docs.html.

Os pacotes do R contêm funções específicas para determinadas tarefas, e estendem a instalação básica do R. Atualmente existem mais de 10000 pacotes disponíveis no CRAN, além de diversos outros hospedados em sites como Github, por exemplo.

Ao instalar o R, os seguintes pacotes já vêm instalados (fazem parte do chamado “R core”):

 [1] "base"       "boot"       "class"      "cluster"    "codetools" 
 [6] "compiler"   "datasets"   "foreign"    "graphics"   "grDevices" 
[11] "grid"       "KernSmooth" "lattice"    "MASS"       "Matrix"    
[16] "methods"    "mgcv"       "nlme"       "nnet"       "parallel"  
[21] "rpart"      "spatial"    "splines"    "stats"      "stats4"    
[26] "survival"   "tcltk"      "tools"      "utils"     

No entanto, nem todos são carregados na inicialização do R. Por padrão, apenas os seguintes pacotes são carregados automaticamente:

[1] "graphics"  "grDevices" "datasets"  "utils"     "methods"   "base"     

Para listar os pacotes carregados, use a função

search()

Note que o primeiro elemento, .GlobalEnv, será sempre carregado pois ele é o ambiente que irá armazenar (e deixar disponível) os objetos criados pelo usuário. Para carregar um pacote instalado, usamos a função library(), por exemplo

library(lattice)
search()

Isso tornará todas as funções do pacote lattice disponíveis para uso.

Para instalar um pacote usamos a função install.packages(). Sabendo o nome do pacote, por exemplo, mvtnorm, fazemos

install.packages("mvtnorm")

Se o diretório padrão de instalação de um pacote for de acesso restrito (root por exemplo), o R irá perguntar se você gostaria de instalar o pacote em uma biblioteca pessoal, e sugerirá um diretório que possui as permissões necessárias. Você pode se antecipar e já definir e criar um diretório na sua pasta pessoal, e instalar os pacotes sempre nesse local. Por exemplo, defina ~/R/library como sua biblioteca pessoal. Para instalar os pacotes sempre nesse diretório faça:

install.packages("mvtnorm", lib = "~/R/library")

Para verificar as bibliotecas disponíveis e se existem pacotes para serem atualizados, use

packageStatus()

Para atualizar automaticamente todos os pacotes faça

update.packages(ask = FALSE)

2.3 Criando uma função

A ideia original do R é transformar usuários em programadores

“… to turn ideas into software, quickly and faithfully.”

– John M. Chambers.

Criar funções para realizar trabalhos específicos é um dos grandes poderes do R.

Por exemplo, podemos criar a famosa função

ola.mundo <- function(){
    writeLines("Olá mundo")
}

E chama-la através de

ola.mundo()
Olá mundo

A função acima não permite alterar o resultado da saída. Podemos fazer isso incluindo um argumento

ola.mundo <- function(texto){
    writeLines(texto)
}

E fazer por exemplo

ola.mundo("Funções são legais")
Funções são legais

(Veremos detalhes de funções mais adiante)

Exercícios

1. Usando a função runif() gere \(30\) números aleatórios entre:
   • 0 e 1
   • -5 e 5
   • 10 e 500

alternando a posição dos argumentos da função.

2. Veja o help da função (?) "+"
3. Crie uma função para fazer a soma de dois números: x e y
4. Crie uma função para simular a jogada de um dado.
5. Crie uma função para simular a jogada de dois dados.

2.4 Objetos

O que é um objeto?

• Um símbolo ou uma variável capaz de armazenar qualquer valor ou estrutura de dados.

Por quê objetos?

• Uma maneira simples de acessar os dados armazenados na memória (o R não permite acesso direto à memória).

Programação:

• Objetos \(\Rightarrow\) Classes \(\Rightarrow\) Métodos.

“Tudo no R é um objeto.”

“Todo objeto no R tem uma classe.”

• Classe: é a definição de um objeto. Descreve a forma do objeto e como ele será manipulado pelas diferentes funções.
• Método: são funções genéricas que executam suas tarefas de acordo com cada classe. Duas das funções genéricas mais importantes são:
  • summary().
  • plot().

Veja o resultado de

methods(summary)
methods(plot)

(Veremos mais detalhes adiante).

A variável x recebe o valor \(2\) (tornando-se um objeto dentro do R):

x <- 2

O símbolo <- é chamado de operador de atribuição. Ele serve para atribuir valores a objetos, e é formado pelos símbolos < e -, obrigatoriamente sem espaços.

Para ver o conteúdo do objeto:

x
[1] 2

Observação: O símbolo = pode ser usado no lugar de <- mas não é recomendado.

Quando você faz

x <- 2

está fazendo uma declaração, ou seja, declarando que a variável x irá agora se tornar um objeto que armazena o número 2. As declarações podem ser feitas uma em cada linha

x <- 2
y <- 4

ou separadas por ;

x <- 2; y <- 4

Operações matemáticas em objetos:

x + x
[1] 4

Objetos podem armazenar diferentes estruturas de dados:

y <- runif(10)
y
 [1] 0.6249965 0.8821655 0.2803538 0.3984879 0.7625511 0.6690217 0.2046122
 [8] 0.3575249 0.3594751 0.6902905

Note que cada objeto só pode armazenar uma estrutura (um número ou uma sequência de valores) de cada vez! (Aqui, o valor \(4\) que estava armazenado em y foi sobrescrito pelos valores acima).

2.4.1 Nomes de objetos

• Podem ser formados por letras, números, “_”, e “.”.
• Não podem começar com número e/ou ponto.
• Não podem conter espaços.
• Evite usar acentos.
• Evite usar nomes de funções como:

c q t C D F I T diff df data var pt

• O R é case-sensitive, portanto:

dados \(\neq\) Dados \(\neq\) DADOS.

2.4.2 Gerenciando a área de trabalho

Liste os objetos criados com a função ls():

ls()

Para remover apenas um objeto:

rm(x)

Para remover outros objetos:

rm(x, y)

Para remover todos os objetos:

rm(list = ls())

Cuidado! O comando acima apaga todos os objetos na sua área de trabalho sem perguntar. Depois só é possível recuperar os objetos ao rodar o script novamente.

Exercícios

1. Armazene o resultado da equação \(32 + 16^2 - 25^3\) no objeto x.
2. Divida x por \(345\) e armazene em y.
3. Crie um objeto (com o nome que você quiser) para armazenar \(30\) valores aleatórios de uma distribuição uniforme entre \(10\) e \(50\).
4. Remova o objeto y.
5. Remova os demais objetos de uma única vez.
6. Procure a função utilizada para gerar numeros aleatórios de uma distribuição de Poisson, e gere \(100\) valores para a VA \(X \sim \text{Poisson}(5)\).

2.5 Tipos e classes de objetos

Para saber como trabalhar com dados no R, é fundamental entender as possíveis estruturas (ou tipos) de dados possíveis. O formato mais básico de dados são os vetores, e a partir deles, outras estruturas mais complexas podem ser construídas. O R possui dois tipos básicos de vetores:

• Vetores atômicos: existem seis tipos básicos:

  • double.
  • integer.
  • character.
  • logical.
  • complex.
  • raw.

  Os tipos integer e double são chamados conjuntamente de numeric.

• Listas: também chamadas de vetores recursivos pois listas podem conter outras listas.

A principal diferença entre vetores atômicos e listas é que o primeiro é homogêneo (cada vetor só pode conter um tipo), enquanto que o segundo pode ser heterogêneo (cada vetor pode conter mais de um tipo).

Um vetor atômico só pode conter elementos de um mesmo tipo.

Um vetor, como o próprio nome diz, é uma estrutura unidimensional, mas na maioria das vezes iremos trabalhar com estruturas de dados bidimensionais (linhas e colunas). Portanto diferentes estruturas (com diferentes dimensões) podem ser criadas a partir dos vetores atômicos. Quando isso acontece, temos o que é chamado de classe de um objeto. Embora os vetores atômicos só possuam seis tipos básicos, existe um número muito grande de classes, e novas são inventadas todos os dias. E mesmo que um objeto seja de qualquer classe, ele sempre será de um dos seis tipos básicos (ou uma lista).

Para verificar o tipo de um objeto, usamos a função typeof(), enquanto que a classe é verificada com a função class(). Vejamos alguns exemplos:

## double
x <- c(2, 4, 6)
typeof(x)
[1] "double"
class(x)
[1] "numeric"
## integer
x <- c(2L, 4L, 6L)
typeof(x)
[1] "integer"
class(x)
[1] "integer"
## character
x <- c("a", "b", "c")
typeof(x)
[1] "character"
class(x)
[1] "character"
## logical
x <- c(TRUE, FALSE, TRUE)
typeof(x)
[1] "logical"
class(x)
[1] "logical"
## complex
x <- c(2 + 1i, 4 + 1i, 6 + 1i)
typeof(x)
[1] "complex"
class(x)
[1] "complex"
## raw
x <- raw(3)
typeof(x)
[1] "raw"
class(x)
[1] "raw"

2.5.1 Vetores numéricos

Características:

• Coleção ordenada de valores.
• Estrutura unidimensional.

Usando a função c() para criar vetores:

num <- c(10, 5, 2, 4, 8, 9)
num
[1] 10  5  2  4  8  9
typeof(num)
[1] "double"
class(num)
[1] "numeric"

Por que numeric e não integer?

x <- c(10L, 5L, 2L, 4L, 8L, 9L)
x
[1] 10  5  2  4  8  9
typeof(x)
[1] "integer"
class(x)
[1] "integer"

Para forçar a representação de um número para inteiro é necessário usar o sufixo L.

Note que a diferença entre numeric e integer também possui impacto computacional, pois o armazenamento de números inteiros ocupa menos espaço na memória. Dessa forma, esperamos que o vetor x acima ocupe menos espaço na memória do que o vetor num, embora sejam aparentemente idênticos. Veja:

object.size(num)
96 bytes
object.size(x)
80 bytes

A diferença pode parecer pequena, mas pode ter um grande impacto computacional quando os vetores são formados por milhares ou milhões de números.

2.5.1.1 Representação numérica dentro do R

Os números que aparecem na tela do console do R são apenas representações simplificadas do número real armazenado na memória. Por exemplo,

x <- runif(10)
x
 [1] 0.2875775 0.7883051 0.4089769 0.8830174 0.9404673 0.0455565 0.5281055
 [8] 0.8924190 0.5514350 0.4566147

O objeto x contém números como 0.2875775, 0.7883051, etc, que possuem 7 casas decimais, que é o padrão do R. O número de casas decimais é controlado pelo argumento digits da função options(). Para visualizar essa opção, use

getOption("digits")
[1] 7

Note que esse valor de 7 é o número de dígitos significativos, e pode variar conforme a sequência de números. Por exemplo,

y <- runif(10)
y
 [1] 0.069360916 0.817775199 0.942621732 0.269381876 0.169348123 0.033895622
 [7] 0.178785004 0.641665366 0.022877743 0.008324827

possui valores com 9 casas decimais. Isto é apenas a representação do número que aparece na tela. Internamente, cada número é armazenado com uma precisão de 64 bits. Como consequência, cada número possui uma acurácia de até 16 dígitos significativos. Isso pode introduzir algum tipo de erro, por exemplo:

sqrt(2)^2 - 2
[1] 4.440892e-16
print(sqrt(2)^2, digits = 22)
[1] 2.000000000000000444089

não é exatamente zero, pois a raíz quadrada de 2 não pode ser armazenada com toda precisão com “apenas” 16 dígitos significativos. Esse tipo de erro é chamado de erro de ponto flutuante, e as operações nessas condições são chamadas de aritmética de ponto flutuante. Para mais informações sobre esse assunto veja What Every Computer Scientist Should Know About Floating-Point Arithmetic e Why doesn’t R think these numbers are equal?.

No R os números podem ser representados com até 22 casas decimais. Você pode ver o número com toda sua precisão usando a função print() e especificando o número de casas decimais com o argumento digits (de 1 a 22).

print(x, digits = 1)
 [1] 0.29 0.79 0.41 0.88 0.94 0.05 0.53 0.89 0.55 0.46
print(x, digits = 7) # padrão
 [1] 0.2875775 0.7883051 0.4089769 0.8830174 0.9404673 0.0455565 0.5281055
 [8] 0.8924190 0.5514350 0.4566147
print(x, digits = 22)
 [1] 0.28757752012461423873901 0.78830513544380664825439
 [3] 0.40897692181169986724854 0.88301740400493144989014
 [5] 0.94046728429384529590607 0.04555649938993155956268
 [7] 0.52810548804700374603271 0.89241904439404606819153
 [9] 0.55143501446582376956940 0.45661473530344665050507

Também é possível alterar a representação na tela para o formato científico, usando a função format()

format(x, scientific = TRUE)
 [1] "2.875775e-01" "7.883051e-01" "4.089769e-01" "8.830174e-01" "9.404673e-01"
 [6] "4.555650e-02" "5.281055e-01" "8.924190e-01" "5.514350e-01" "4.566147e-01"

Nessa representação, o valor 2.875775e-01 = \(2.875775 \times 10^{-01}\) = \(0.2875775\).

2.5.1.2 Sequências de números

Usando a função seq()

seq(1, 10)
 [1]  1  2  3  4  5  6  7  8  9 10

Ou 1:10 gera o mesmo resultado. Para a sequência variar em \(2\)

seq(from = 1, to = 10, by = 2)
[1] 1 3 5 7 9

Para obter \(15\) valores entre \(1\) e \(10\)

seq(from = 1, to = 10, length.out = 15)
 [1]  1.000000  1.642857  2.285714  2.928571  3.571429  4.214286  4.857143
 [8]  5.500000  6.142857  6.785714  7.428571  8.071429  8.714286  9.357143
[15] 10.000000

Usando a função rep()

rep(1, 10)
 [1] 1 1 1 1 1 1 1 1 1 1

Para gerar um sequência várias vezes

rep(c(1, 2, 3), times = 5)
 [1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

Para repetir um número da sequência várias vezes

rep(c(1, 2, 3), each = 5)
 [1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3

2.5.1.3 Operações matemáticas em vetores numéricos

Operações podem ser feitas entre um vetor e um número:

num * 2
[1] 20 10  4  8 16 18

E também entre vetores de mesmo comprimento ou com comprimentos múltiplos:

num * num
[1] 100  25   4  16  64  81
num + c(2, 4, 1)
[1] 12  9  3  6 12 10

2.5.1.4 A Regra da Reciclagem

Agora tente:

num + c(2, 4, 1, 3)

2.5.2 Outros tipos de vetores

Vetores também podem ter outros tipos:

• Vetor de caracteres:

caracter <- c("brava", "joaquina", "armação")
caracter
[1] "brava"    "joaquina" "armação" 
typeof(caracter)
[1] "character"
class(caracter)
[1] "character"

• Vetor lógico:

logico <- caracter == "armação"
logico
[1] FALSE FALSE  TRUE
typeof(logico)
[1] "logical"
class(logico)
[1] "logical"

ou

logico <- num > 4
logico
[1]  TRUE  TRUE FALSE FALSE  TRUE  TRUE

No exemplo anterior, a condição num > 4 é uma expressão condicional, e o símbolo > um operador lógico. Os operadores lógicos utilizados no R são:

Operador	Sintaxe	Teste
<	a < b	a é menor que b?
<=	a <= b	a é menor ou igual a b?
>	a > b	a é maior que b
>=	a >= b	a é maior ou igual a b?
==	a == b	a é igual a b?
!=	a != b	a é diferente de b?
%in%	a %in% c(a, b)	a está contido no vetor c(a, b)?

2.5.3 Misturando classes de objetos

Algumas vezes isso acontece por acidente, mas também pode acontecer de propósito.

O que acontece aqui?

w <- c(5L, "a")
x <- c(1.7, "a")
y <- c(TRUE, 2)
z <- c("a", T)

Lembre-se da regra:

Um vetor só pode conter elementos do mesmo tipo!

Quando objetos de diferentes tipos são misturados, ocorre a coerção, para que cada elemento possua a mesma classe.

Nos exemplos acima, nós vemos o efeito da coerção implícita, quando o R tenta representar todos os objetos de uma única forma.

Nós podemos forçar um objeto a mudar de classe, através da coerção explícita, realizada pelas funções as.*:

x <- 0:6
typeof(x)
[1] "integer"
class(x)
[1] "integer"
as.numeric(x)
[1] 0 1 2 3 4 5 6
as.logical(x)
[1] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
as.character(x)
[1] "0" "1" "2" "3" "4" "5" "6"
as.factor(x)
[1] 0 1 2 3 4 5 6
Levels: 0 1 2 3 4 5 6

De ?logical:

 Logical vectors are coerced to integer vectors in contexts where a
 numerical value is required, with ‘TRUE’ being mapped to ‘1L’,
 ‘FALSE’ to ‘0L’ and ‘NA’ to ‘NA_integer_’.

(x <- c(FALSE, TRUE))
[1] FALSE  TRUE
class(x)
[1] "logical"
as.numeric(x)
[1] 0 1

Algumas vezes não é possível fazer a coerção, então:

x <- c("a", "b", "c")
as.numeric(x)
Warning: NAs introduced by coercion
[1] NA NA NA
as.logical(x)
[1] NA NA NA

2.5.4 Valores perdidos e especiais

Valores perdidos devem ser definidos como NA (not available):

perd <- c(3, 5, NA, 2)
perd
[1]  3  5 NA  2
class(perd)
[1] "numeric"

Podemos testar a presença de NAs com a função is.na():

is.na(perd)
[1] FALSE FALSE  TRUE FALSE

Ou:

any(is.na(perd))
[1] TRUE

Outros valores especiais são:

• NaN (not a number) - exemplo: 0/0
• -Inf e Inf - exemplo: 1/0

A função is.na() também testa a presença de NaNs:

perd <- c(-1,0,1)/0
perd
[1] -Inf  NaN  Inf
is.na(perd)
[1] FALSE  TRUE FALSE

A função is.infinite() testa se há valores infinitos

is.infinite(perd)
[1]  TRUE FALSE  TRUE

Exercícios

1. Crie um objeto com os valores 54, 0, 17, 94, 12.5, 2, 0.9, 15.
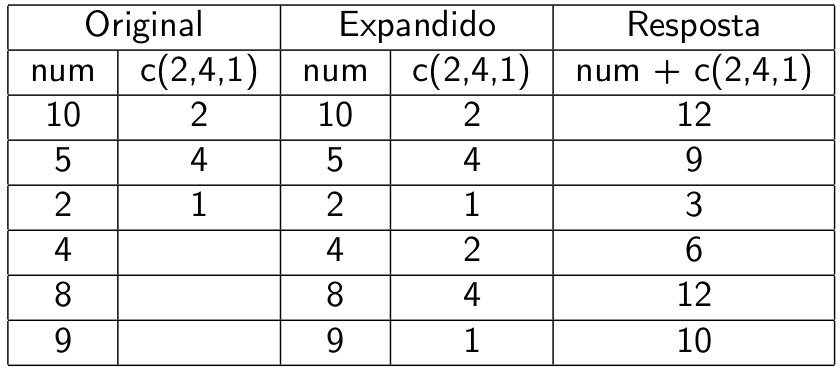
   1. Some o objeto acima com os valores 5, 6, e depois com os valores 5, 6, 7.
2. Construa um único objeto com as letras: A, B, e C, repetidas cada uma 15, 12, e 8 vezes, respectivamente.
   1. Mostre na tela, em forma de verdadeiro ou falso, onde estão as letras B nesse objeto.
   2. Veja a página de ajuda da função sum() e descubra como fazer para contar o número de letras B neste vetor (usando sum()).
3. Crie um objeto com 100 valores aleatórios de uma distribuição uniforme \(U(0,1)\). Conte quantas vezes aparecem valores maiores ou iguais a 0,5.
4. Calcule as 50 primeiras potências de 2, ou seja, \(2, 2^2, 2^3, \ldots, 2^{50}\).
   1. Calcule o quadrado dos números inteiros de 1 a 50, ou seja, \(1^2, 2^2, 3^2, \ldots, 50^2\).
   2. Quais pares são iguais, ou seja, quais números inteiros dos dois exercícios anteriores satisfazem a condição \(2^n = n^2\)?
   3. Quantos pares existem?
5. Calcule o seno, coseno e a tangente para os números variando de \(0\) a \(2\pi\), com distância de \(0.1\) entre eles. (Use as funções sin(), cos(), tan()).
   1. Calcule a tangente usando a relação \(\tan(x) = \sin(x)/\cos(x)\).
   2. Calcule as diferenças das tangentes calculadas pela função do R e pela razão acima.
   3. Quais valores são exatamente iguais?
   4. Qual a diferença máxima (em módulo) entre eles? Qual é a causa dessa diferença?

2.6 Outras classes

Como mencionado na seção anterior, o R possui 6 tipos básicos de estrutura de dados, mas diversas classes podem ser construídas a partir destes tipos básicos. Abaixo, veremos algumas das mais importantes.

2.6.1 Fator

Os fatores são parecidos com caracteres no R, mas são armazenados e tratados de maneira diferente.

Características:

• Coleção de categorias ou níveis (levels).
• Estrutura unidimensional.

Utilizando as funções factor() e c():

fator <- factor(c("alta","baixa","baixa","media",
                  "alta","media","baixa","media","media"))
fator
[1] alta  baixa baixa media alta  media baixa media media
Levels: alta baixa media
class(fator)
[1] "factor"
typeof(fator)
[1] "integer"

Note que o objeto é da classe factor, mas seu tipo básico é integer! Isso significa que cada categoria única é identificada internamente por um número, e isso faz com que os fatores possuam uma ordenação, de acordo com as categorias únicas. Por isso existe a identificação dos Levels (níveis) de um fator.

Veja o que acontece quando “remover a classe” desse objeto

unclass(fator)
[1] 1 2 2 3 1 3 2 3 3
attr(,"levels")
[1] "alta"  "baixa" "media"

Fatores podem ser convertidos para caracteres, e também para números inteiros

as.character(fator)
[1] "alta"  "baixa" "baixa" "media" "alta"  "media" "baixa" "media" "media"
as.integer(fator)
[1] 1 2 2 3 1 3 2 3 3

Caso haja uma hierarquia, os níveis dos fatores podem ser ordenados explicitamente através do argumento levels:

fator <- factor(c("alta","baixa","baixa","media",
                  "alta","media","baixa","media","media"),
                levels = c("alta","media","baixa"))
fator
[1] alta  baixa baixa media alta  media baixa media media
Levels: alta media baixa
typeof(fator)
[1] "integer"
class(fator)
[1] "factor"

Além disso, os níveis dos fatores podem também ser explicitamente ordenados

fator <- factor(c("alta","baixa","baixa","media",
                  "alta","media","baixa","media","media"),
                levels = c("baixa", "media", "alta"),
                ordered = TRUE)
fator
[1] alta  baixa baixa media alta  media baixa media media
Levels: baixa < media < alta
typeof(fator)
[1] "integer"
class(fator)
[1] "ordered" "factor" 

Veja que um objeto pode ter mais de uma classe. Isso geralmente só será útil em casos especificos.

As seguintes funções são úteis para verificar os níveis e o número de níveis de um fator:

levels(fator)
[1] "baixa" "media" "alta" 
nlevels(fator)
[1] 3

2.6.2 Matriz

Matrizes são vetores que podem ser dispostos em duas dimensões.

Características:

• Podem conter apenas um tipo de informação (números, caracteres)
• Estrutura bidimensional

Utilizando a função matrix():

matriz <- matrix(1:12, nrow = 3, ncol = 4)
matriz
     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12
class(matriz)
[1] "matrix" "array" 
typeof(matriz)
[1] "integer"

Alterando a ordem de preenchimento da matriz (por linhas):

matriz <- matrix(1:12, nrow = 3, ncol = 4, byrow = TRUE)
matriz
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12

Para verificar a dimensão da matriz:

dim(matriz)
[1] 3 4

Adicionando colunas com cbind()

cbind(matriz, rep(99, 3))
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4   99
[2,]    5    6    7    8   99
[3,]    9   10   11   12   99

Adicionando linhas com rbind()

rbind(matriz, rep(99, 4))
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12
[4,]   99   99   99   99

Matrizes também podem ser criadas a partir de vetores adicionando um atributo de dimensão, por exemplo,

m <- 1:10
m
 [1]  1  2  3  4  5  6  7  8  9 10
class(m)
[1] "integer"
dim(m)
NULL
dim(m) <- c(2, 5)
m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    5    7    9
[2,]    2    4    6    8   10
class(m)
[1] "matrix" "array" 
typeof(m)
[1] "integer"

2.6.2.1 Operações matemáticas em matrizes

Matriz multiplicada por um escalar

matriz * 2
     [,1] [,2] [,3] [,4]
[1,]    2    4    6    8
[2,]   10   12   14   16
[3,]   18   20   22   24

Multiplicação de matrizes (observe as dimensões!)

matriz2 <- matrix(1, nrow = 4, ncol = 3)
matriz %*% matriz2
     [,1] [,2] [,3]
[1,]   10   10   10
[2,]   26   26   26
[3,]   42   42   42

2.6.3 Array

Um array é a forma mais geral de uma matriz, pois pode ter \(n\) dimensões.

Características:

• Estrutura \(n\)-dimensional.
• Assim como as matrizes, podem conter apenas um tipo de informação (números, caracteres).

Para criar um array, usamos a função array(), passando como primeiro argumento um vetor atômico, e especificamos a dimensão com o argumento dim. Por exemplo, para criar um objeto com 3 dimensões \(2 \times 2 \times 3\), fazemos

ar <- array(1:12, dim = c(2, 2, 3))
ar
, , 1

     [,1] [,2]
[1,]    1    3
[2,]    2    4

, , 2

     [,1] [,2]
[1,]    5    7
[2,]    6    8

, , 3

     [,1] [,2]
[1,]    9   11
[2,]   10   12

Similarmente, um array de 2 dimensões \(3 \times 2 \times 2\) é obtido com

ar <- array(1:12, dim = c(3, 2, 2))
ar
, , 1

     [,1] [,2]
[1,]    1    4
[2,]    2    5
[3,]    3    6

, , 2

     [,1] [,2]
[1,]    7   10
[2,]    8   11
[3,]    9   12

2.6.4 Lista

Como já vimos, uma lista não é uma “classe” propriamente dita, mas sim um tipo de estrutura de dados básico, ao lado dos vetores atômicos. E, assim como os vetores atômicos, listas são estruturas unidimensionais. A grande diferença é que listas agrupam objetos de diferentes tipos, inclusive outras listas.

Características:

• Pode combinar uma coleção de objetos de diferentes tipos ou classes (é um tipo básico de vetor, assim como os vetores atômicos).
• Estrutura “unidimensional”: apenas o número de elementos na lista é contado.

Por exemplo, podemos criar uma lista com uma sequência de números, um caracter e outra lista.

lista <- list(1:30, "R", list(TRUE, FALSE))
lista
[[1]]
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
[26] 26 27 28 29 30

[[2]]
[1] "R"

[[3]]
[[3]][[1]]
[1] TRUE

[[3]][[2]]
[1] FALSE
class(lista)
[1] "list"
typeof(lista)
[1] "list"

Para melhor visualizar a estrutura dessa lista (ou de qualquer outro objeto) podemos usar a função str()

str(lista)
List of 3
 $ : int [1:30] 1 2 3 4 5 6 7 8 9 10 ...
 $ : chr "R"
 $ :List of 2
  ..$ : logi TRUE
  ..$ : logi FALSE

Note que de fato é uma estrutura unidimensional

dim(lista)
NULL
length(lista)
[1] 3

Listas podem armazenar objetos de diferentes classes e dimensões, por exemplo, usando objetos criados anteriormente

lista <- list(fator, matriz)
lista
[[1]]
[1] alta  baixa baixa media alta  media baixa media media
Levels: baixa < media < alta

[[2]]
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12
length(lista)
[1] 2

2.6.5 Data frame

Data frame é a versão bidimensional de uma lista. Data frames são listas, mas onde cada componente deve ter obrigatoriamente o mesmo comprimento. Cada vetor da lista vira uma coluna em um data frame, permitindo então que as “colunas” sejam de diferentes tipos.

Os data frames são as estruturas mais comuns para se trabalhar com dados no R.

Características:

• Uma lista de vetores e/ou fatores, de mesmo comprimento.
• Pode conter diferentes tipos de dados (numérico, fator, …).
• Estrutura bidimensional.

Utilizando a função data.frame():

da <- data.frame(nome = c("João", "José", "Maria"),
                 sexo = c("M", "M", "F"),
                 idade = c(32, 34, 30))
da
   nome sexo idade
1  João    M    32
2  José    M    34
3 Maria    F    30
class(da)
[1] "data.frame"
typeof(da)
[1] "list"
dim(da)
[1] 3 3

Veja os detalhes com str()

str(da)
'data.frame':   3 obs. of  3 variables:
 $ nome : chr  "João" "José" "Maria"
 $ sexo : chr  "M" "M" "F"
 $ idade: num  32 34 30

Em versões anteriores a função data.frame() convertia caracteres para fator automaticamente mas o padrão mudou. Use o argumento stringsAsFactors para controlar este comportamento.

da <- data.frame(nome = c("João", "José", "Maria"),
                 sexo = c("M", "M", "F"),
                 idade = c(32, 34, 30))
da 
   nome sexo idade
1  João    M    32
2  José    M    34
3 Maria    F    30
str(da)
'data.frame':   3 obs. of  3 variables:
 $ nome : chr  "João" "José" "Maria"
 $ sexo : chr  "M" "M" "F"
 $ idade: num  32 34 30

da <- data.frame(nome = c("João", "José", "Maria"),
                 sexo = c("M", "M", "F"),
                 idade = c(32, 34, 30),
                 stringsAsFactors = FALSE)
str(da)
'data.frame':   3 obs. of  3 variables:
 $ nome : chr  "João" "José" "Maria"
 $ sexo : chr  "M" "M" "F"
 $ idade: num  32 34 30
    
da <- data.frame(nome = c("João", "José", "Maria"),
                 sexo = c("M", "M", "F"),
                 idade = c(32, 34, 30),
                 stringsAsFactors = TRUE)
str(da)
'data.frame':   3 obs. of  3 variables:
 $ nome : Factor w/ 3 levels "João","José",..: 1 2 3
 $ sexo : Factor w/ 2 levels "F","M": 2 2 1
 $ idade: num  32 34 30

Data frames podem ser formados com objetos criados anteriormente, desde que tenham o mesmo comprimento:

length(num)
[1] 6
length(fator)
[1] 9
db <- data.frame(numerico = c(num, NA, NA, NA),
                 fator = fator)
db
  numerico fator
1       10  alta
2        5 baixa
3        2 baixa
4        4 media
5        8  alta
6        9 media
7       NA baixa
8       NA media
9       NA media
str(db)
'data.frame':   9 obs. of  2 variables:
 $ numerico: num  10 5 2 4 8 9 NA NA NA
 $ fator   : Ord.factor w/ 3 levels "baixa"<"media"<..: 3 1 1 2 3 2 1 2 2

Algumas vezes pode ser necessário converter um data frame para uma matriz. Existem duas opções:

as.matrix(db)
      numerico fator  
 [1,] "10"     "alta" 
 [2,] " 5"     "baixa"
 [3,] " 2"     "baixa"
 [4,] " 4"     "media"
 [5,] " 8"     "alta" 
 [6,] " 9"     "media"
 [7,] NA       "baixa"
 [8,] NA       "media"
 [9,] NA       "media"
data.matrix(db)
      numerico fator
 [1,]       10     3
 [2,]        5     1
 [3,]        2     1
 [4,]        4     2
 [5,]        8     3
 [6,]        9     2
 [7,]       NA     1
 [8,]       NA     2
 [9,]       NA     2

Geralmente é o resultado de data.matrix() o que você está procurando.

Lembre que os níveis de um fator são armazenados internamente como números: \(1^\circ\) nível = 1, \(2^\circ\) nível = 2, \(\ldots\).

fator
[1] alta  baixa baixa media alta  media baixa media media
Levels: baixa < media < alta
str(fator)
 Ord.factor w/ 3 levels "baixa"<"media"<..: 3 1 1 2 3 2 1 2 2
as.numeric(fator)
[1] 3 1 1 2 3 2 1 2 2

2.7 Atributos de objetos

Um atributo é um pedaço de informação que pode ser “anexado” à qualquer objeto, e não irá interferir nos valores daquele objeto. Os atributos podem ser vistos como “metadados”, alguma descrição associada à um objeto. Os principais atributos são:

• names
• dimnames
• dim
• class

Alguns atributos também podem ser visualizados de uma só vez através da função attributes().

Por exemplo, considere o seguinte vetor

x <- 1:6
attributes(x)
NULL

Mostra que o objeto x não possui nenhum atributo. Mas podemos definir nomes, por exemplo, para cada componente desse vetor

names(x)
NULL
names(x) <- c("um", "dois", "tres", "quatro", "cinco", "seis")
names(x)
[1] "um"     "dois"   "tres"   "quatro" "cinco"  "seis"  
attributes(x)
$names
[1] "um"     "dois"   "tres"   "quatro" "cinco"  "seis"  

Nesse caso específico, o R irá mostrar os nomes acima dos componentes, mas isso não altera como as operaçõs serão realizadas.

x
    um   dois   tres quatro  cinco   seis 
     1      2      3      4      5      6 
x + 2
    um   dois   tres quatro  cinco   seis 
     3      4      5      6      7      8 

Os nomes então podem ser definidos através da função auxiliar names(), sendo assim, também podemos remover esse atributo declarando ele como nulo.

names(x) <- NULL
attributes(x)
NULL
x
[1] 1 2 3 4 5 6

Outros atributos também podem ser definidos de maneira similar. Veja os exemplos abaixo:

length(x)
[1] 6
## Altera o comprimento (preenche com NA)
length(x) <- 10
x
 [1]  1  2  3  4  5  6 NA NA NA NA
## Altera a dimensão
length(x) <- 6
dim(x)
NULL
dim(x) <- c(3, 2)
x
     [,1] [,2]
[1,]    1    4
[2,]    2    5
[3,]    3    6
attributes(x)
$dim
[1] 3 2
## Remove dimensão
dim(x) <- NULL
x
[1] 1 2 3 4 5 6

Assim como vimos em data frames, listas também podem ter nomes

x <- list(Curitiba = 1, Paraná = 2, Brasil = 3)
x
$Curitiba
[1] 1

$Paraná
[1] 2

$Brasil
[1] 3
names(x)
[1] "Curitiba" "Paraná"   "Brasil"  

Podemos também associar nomes às linhas e colunas de uma matriz:

matriz
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12
attributes(matriz)
$dim
[1] 3 4
rownames(matriz) <- c("A","B","C")
colnames(matriz) <- c("T1","T2","T3","T4")
matriz
  T1 T2 T3 T4
A  1  2  3  4
B  5  6  7  8
C  9 10 11 12
attributes(matriz)
$dim
[1] 3 4

$dimnames
$dimnames[[1]]
[1] "A" "B" "C"

$dimnames[[2]]
[1] "T1" "T2" "T3" "T4"

Para data frames existe uma função especial para os nomes de linhas, row.names(). Data frames também não possuem nomes de colunas, apenas nomes, já que é um caso particular de lista. Então para verificar/alterar nomes de colunas de um data frame também use names().

da
   nome sexo idade
1  João    M    32
2  José    M    34
3 Maria    F    30
attributes(da)
$names
[1] "nome"  "sexo"  "idade"

$class
[1] "data.frame"

$row.names
[1] 1 2 3
names(da)
[1] "nome"  "sexo"  "idade"
row.names(da)
[1] "1" "2" "3"

Um resumo das funções para alterar/acessar nomes de linhas e colunas em matrizes e data frames.

Classe	Nomes de colunas	Nomes de linhas
data.frame	names()	row.names()
matrix	colnames()	rownames()

Exercícios

1. Crie um objeto para armazenar a seguinte matriz \[\left[ \begin{array}{ccc} 2 & 8 & 4 \\ 0 & 4 & 1 \\ 9 & 7 & 5 \end{array} \right]\]
2. Atribua nomes para as linhas e colunas dessa matriz.
3. Crie uma lista (não nomeada) com dois componentes: (1) um vetor com as letras A, B, e C, repetidas 2, 5, e 4 vezes respectivamente; e (2) a matriz do exemplo anterior.
4. Atribua nomes para estes dois componentes da lista.
5. Inclua mais um componente nesta lista, com o nome de fator, e que seja um vetor da classe factor, idêntico ao objeto caracter criado acima (que possui apenas os nomes brava, joaquina, armação).
6. Crie um data frame para armazenar duas variáveis: local (A, B, C, D), e contagem (42, 34, 59 e 18).
7. Crie um data frame com as seguintes colunas:

• Nome
• Sobrenome
• Se possui animal de estimação
• Caso possua, dizer o número de animais (caso contrário, colocar 0)

Para criar o data frame, a primeira linha deve ser preenchida com as suas próprias respostas (use a função data.frame()). Depois, pergunte essas mesmas questões para dois colegas ao seu lado, e adicione as respostas deles à esse data frame (use rbind()). Acresente mais uma coluna com o nome do time de futebol de cada um.

Referências

Para mais detalhes e exemplos dos assuntos abordados aqui, veja Grolemund (2014). Uma abordagem mais avançada e detalhada sobre programação orientada a objetos no R pode ser consultada em Wickham (2015).

Grolemund, Garrett. 2014. Hands-On Programming with R - Write Your Own Functions and Simulations. O’Reily Media. http://shop.oreilly.com/product/0636920028574.do.

Wickham, Hadley. 2015. Advanced R. CRC Press.

References

Grolemund, Garrett. 2014. Hands-On Programming with R - Write Your Own Functions and Simulations. O’Reily Media. http://shop.oreilly.com/product/0636920028574.do.

Wickham, Hadley. 2015. Advanced R. CRC Press.